無理数ってどんな数?
無理数ってどんな数?有理数との違いや身近な例も知りたい
無理数は、分数で表すことができない実数のことです。小数で表すと、終わることなく続き、しかも同じパターンが繰り返されません。
無理数は、分数で表すことができない実数のことです。小数で表すと、終わることなく続き、しかも同じパターンが繰り返されません。
代表的な例は、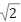 や円周率π、自然対数の底eなど。
や円周率π、自然対数の底eなど。
一見すると抽象的に見えますが、正方形の対角線や円の円周、建築や音楽など、実は身近なところにも無理数はたくさん現れます。
ここでは、無理数とは何か、なぜ存在するのか、そして私たちの身の回りでどのように現れるのかを、分かりやすく解説していきます。
無理数とは何か?定義を確認しよう
無理数とは、分数で表すことができない実数のことです。より正確には「有理数でない実数」と定義されます。
例えば、以下のような数が無理数の代表例です。
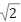 ≈ 1.41421356…
≈ 1.41421356…- π(円周率)≈ 3.14159265…
- e(自然対数の底) ≈ 2.71828182…
これらの数に共通するのは、どんなに頑張っても「分母と分子がいずれも整数の分数」の形で表現できないということです。
身近な例で考えてみよう
一辺が 1 の正方形を考える。対角線の長さはピタゴラスの定理より「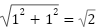 」 となる。この
」 となる。この 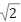 は“実在する長さ”だが、分数では表せない(無理数)。
は“実在する長さ”だが、分数では表せない(無理数)。
無理数は小数で表すと非循環無限小数になります。つまり、小数点以下の数字が永遠に続き、かつ同じパターンを繰り返さない数です。
無理数と有理数の関係
実数の分類
数学では、数を以下のような階層構造で分類します。
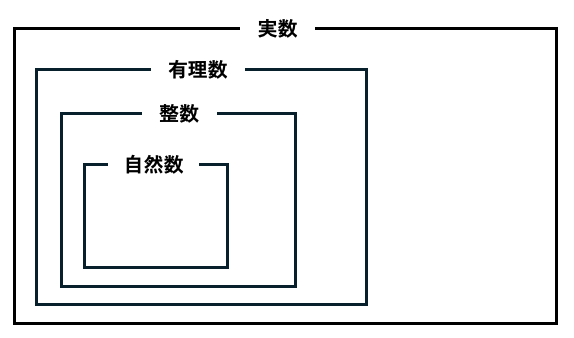
そして、「実数の集合=有理数の集合無理数の集合」という関係が成り立ちます。つまり、すべての実数は有理数か無理数のどちらか一方に分類されるのです。
興味深いことに、無理数は有理数よりもはるかに「多い」のです。どちらも無限に存在するのに「多さ」に違いがあるというのは不思議に聞こえるかもしれませんが、数学では無限にも種類があります。
有理数は「可算無限個」と呼ばれる種類の無限で、これは理論上すべてに番号をつけて1番目、2番目、3番目と順序立てて数え上げることができる無限を意味します。一方、無理数は「非可算無限個」という、どんなに工夫しても番号をつけて数え上げることが不可能な、より大きな種類の無限なのです。
例えば、数直線上の0と1の間という小さな区間を考えてみても、そこには有理数が無限に存在しますが、実は無理数の方が圧倒的に多く、有理数はむしろ無理数の海にポツポツと浮かぶ島のような存在だと考えることができます。この驚くべき事実は19世紀の数学者カントールによって証明され、現在でも数学の最も美しい発見の一つとされています。
有理数の定義
無理数を理解するために、まず有理数の定義を確認しましょう。
有理数とは「2つの整数 a, b を用いて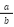 の形で表せる数」のことです。
の形で表せる数」のことです。
有理数の例
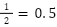
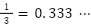 (循環小数)
(循環小数)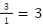 (整数)
(整数)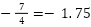 (負の数)
(負の数)
重要な特徴は、有理数を小数で表すと、有限小数または循環小数になることです。
無理数の証明
では、具体的に無理数(違いに素な2つの整数 a, b(b≠0)を用いて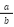 の形で表せる数)が存在するのか、その証明を見ていきましょう。ここでは、
の形で表せる数)が存在するのか、その証明を見ていきましょう。ここでは、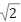 が無理数であることを背理法を用いて証明します。
が無理数であることを背理法を用いて証明します。
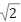 が無理数であることの証明
が無理数であることの証明
-
1. 仮定
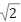 が無理数でない、つまり有理数であると仮定します。
が無理数でない、つまり有理数であると仮定します。
-
2. 有理数の表現
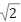 が有理数であるならば、互いに素な(最大公約数が1である)整数 a, b(b≠0)を用いて、
が有理数であるならば、互いに素な(最大公約数が1である)整数 a, b(b≠0)を用いて、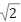
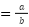 と表すことができます。
と表すことができます。
-
3. 式の変形
この式の両辺を2乗すると、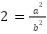 つまり
つまり 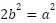 になります。
になります。
-
4. aの性質
2b2 = a2であることから、a2は偶数であることがわかります。a2が偶数であれば、a自身も偶数である必要があります(奇数を2乗すると必ず奇数になるため)。したがって、a はある整数 k を用いて a = 2k と表せます。 -
5. bの性質
a = 2k を2b2 = a2に代入すると、2b2 = (2k)2つまりb2 = 2k2になります。この式から、b2は偶数であることがわかります。b2が偶数であれば、b 自身も偶数である必要があります。 -
6. 矛盾
ここまでの議論で、a は偶数であり、b も偶数であることが示されました。 しかし、これは最初に「a と b は互いに素である」と仮定したことに矛盾します。なぜなら、a も b も偶数であるならば、共通の因数2を持つため、互いに素ではないからです。 -
7. 結論
この矛盾は、「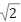 が有理数である」という最初の仮定が間違っていたことを意味します。したがって、
が有理数である」という最初の仮定が間違っていたことを意味します。したがって、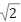 は無理数であると証明されました。
は無理数であると証明されました。
日常生活における無理数
無理数は決して抽象的な概念ではありません。私たちの身の回りに数多く現れています。
正方形の対角線
一辺1(cm)の正方形の対角線は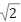 (cm) = 1.414…(cm)です。実際に定規で近い値を測ることはできますが、この長さを正確に測ることは不可能です。
(cm) = 1.414…(cm)です。実際に定規で近い値を測ることはできますが、この長さを正確に測ることは不可能です。
円周率π
直径1(m)の円の円周の長さは π(m) = 3.14159…(m)です。円は日常生活の至る所に現れるため、 πも身近な無理数と言えるでしょう。古くから「3.14」や分数「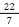 」で近似されてきましたが、これらは近似値であって正確な値ではありません。
」で近似されてきましたが、これらは近似値であって正確な値ではありません。
黄金比
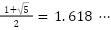 という比率は「黄金比」と呼ばれ、美しい比率として芸術や建築で重用されています。パルテノン神殿の縦横比、ひまわりの種の配列、貝殻の螺旋など、自然界にも頻繁に現れる神秘的な比率です。
という比率は「黄金比」と呼ばれ、美しい比率として芸術や建築で重用されています。パルテノン神殿の縦横比、ひまわりの種の配列、貝殻の螺旋など、自然界にも頻繁に現れる神秘的な比率です。
音楽との関係
音階の周波数比にも無理数が関係しています。12平均律では、隣り合う音の周波数比は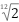 という無理数になります。
という無理数になります。
コンピュータとの関係
デジタル技術が発達した現代でも、無理数は重要な役割を果たしています。コンピュータグラフィックスでの円や曲線の描画、暗号技術、科学計算など、様々な場面で無理数の近似計算が行われています。
これらの例からも分かるように、無理数は「理論上の数」ではなく、私たちの世界を記述するのに欠かせない実在的な数なのです。
まとめ|無理数の意味と大事なポイント
無理数は「分数で表せない実数」
→ 小数で表すと止まらず、繰り返しもない“非循環無限小数”になる。
代表例
→ 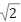 、円周率π、自然対数の底e、黄金比など。
、円周率π、自然対数の底e、黄金比など。
→ 正方形の対角線や円の円周の長さなど、身近な場面に現れる。
有理数との違いを押さえる
→ 有理数は有限小数か循環小数に必ずなる。
→ 無理数はどんな工夫をしても分数の形では表せない。
存在の証明も重要
→ 背理法で「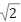 は分数で表せない」ことが示せる。
→ 有理数よりも無理数のほうが“多い”という数学的事実も大切なポイント。
は分数で表せない」ことが示せる。
→ 有理数よりも無理数のほうが“多い”という数学的事実も大切なポイント。
実生活での応用
→ πを用いた円の計算、建築や芸術に現れる黄金比、音楽の周波数比やコンピュータグラフィックスの計算など。
ただ実際の学習では、
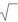 がついていると全部「無理数」だと思ってしまう
がついていると全部「無理数」だと思ってしまう- 有理数と無理数の判定があいまい
- 小数表示からの見分け方を誤る
といった壁に直面する高校生は多いです。そんなときに役立つのが 進研ゼミのAI質問機能(お試し無料)。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「数と式」Q&A一覧
「数と式」Q&A一覧
- 【数と式】「pならばq 」が真のとき,集合Pが集合Qに含まれる理由
- 【数と式】たすきがけのやり方について
- 【数と式】たすきがけはいつ使うのか
- 【数と式】ルートの中が「負の数の2乗」のときの,ルートのはずし方
- 【数と式】因数分解のしかた
- 【数と式】因数分解の式の整理について
- 【数と式】因数分解の式変形について
- 【数と式】因数分解をするときの途中式について
- 【数と式】対称式はどんなとき使うんですか?
- 【数と式】式変形するときの文字の置き換え方
- 【数と式】必要条件・十分条件
- 【数と式】文字を含む式の書き方
- 【数と式】無理数の整数部分,小数部分の求め方
- 【数と式】絶対値と場合分け
- 【数と式】絶対値記号の意味
- 【数と式】絶対値記号を含む方程式・不等式の解き方
- 【数と式】負の値の絶対値の考え方について
- 【数と式】逆・裏・対偶の関係
- 【数と式】連立不等式の解の求め方
- 【数と式】2重根号の計算
- 【数と式】有理数ってどんな数?分数で表せる数の見分け方と無理数との違いが知りたい
- 【数と式】無理数ってどんな数?有理数との違いや身近な例も知りたい














