進研ゼミ高校講座
> Ｑ&Ａトップ
> 数学のＱ&Ａ一覧
> 【数と式】因数分解のしかた

【数と式】因数分解のしかた

因数分解のしかた

3x^2+xy-2y^2+6x+y+3=3x^2+(y+6)x-(2y-3)(y+1)
={3x-(2y-3)}{x+(y+1)}
=(3x-2y+3)(x+y+1)

途中式、だいぶはしょっちゃったんですけど…

答えの前の式から答えの式になる流れはわかるのですが、答えの前の前の式から答えの前の式への流れがわかりません。

展開の公式を利用した因数分解ですか？(あ、でも、因数分解は絶対展開の公式を利用しますよね…(^-^;))

私が知りたいのは、上記の式の因数分解の流れです。
どうしてそのようにまとめるのかを教えてください！

進研ゼミからの回答！

こんにちは。
いただいた質問について、早速回答します。

【質問の確認】

【問題】
次の式を因数分解せよ。
3x²+xy-2y²+6x+y+3

の問題について

【解答解説】

3x²+xy-2y²+6x+y+3
=3x²+(y+6)x-2y²+y+3
=3x²+(y+6)x-(2y²-y-3)

=3x²+(y+6)x-(2y-3)(y+1)　･･････★
={3x-(2y-3)}{x+(y+1)}　･･････★
=(3x-2y+3)(x+y+1)　･･････（答）

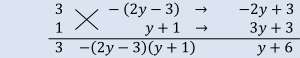
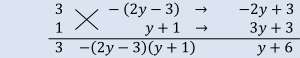
の★の部分の式変形について、ですね。

【解説】

では、わかりやすくする為に、その部分だけを抜き出して、説明しましょう。
3x²+(y+6)x-(2y-3)(y+1)={3x-(2y-3)}{x+(y+1)}と因数分解するには、
「たすきがけ」を使います。その詳しい手順は、次のようになっています。

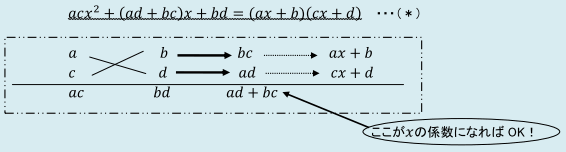
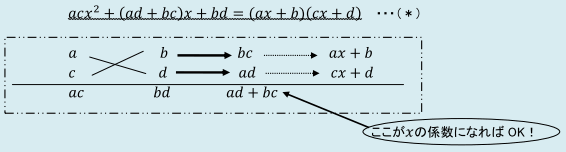
①掛けてx²の係数になる2数を考えます。　→　aとcだね！！

②掛けて定数項bdになる2数を考えます。　→　bとdだね！！

③aとc、bとdをそれぞれ上下に上図のように配置します。

④配置したものを、たすきがけ状に掛け算します。

⑤掛け算した結果は、adを下にbcを上に書きます。

⑥ad+bcを行い、それがxの係数に一致すればOK！！

⑦上段からはax+bを、下段からはcx+dをつくり、（＊）の右辺のように因数分解して完成です！

では、これに沿って 3x²+(y+6)x-(2y-3)(y+1)　を因数分解してみましょう。

①掛けてx²の係数になる2数は？　→　1と3

②掛けて定数項 -(2y-3)(y+1)になる2数は？　→　-(2y-3)と(y+1)

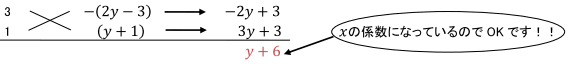
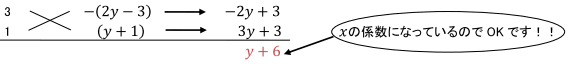
⑦上段から[3x+{-(2y-3)}]={3x-(2y-3)}ができ、下段から{x+(y+1)}ができるので、3x²+(y+6)x-(2y-3)(y+1)={3x-(2y-3)}{x+(y+1)}
と因数分解して完成です！！

さて、③で各2数を配置する際、もし、3と1の上下を逆に配置していたらどうなるでしょう〜？
また、②の2数を(2y-3)と-(y+1)のように、−を逆に配置していたらどうなるでしょう〜？これらはいずれも、ad+bcの値がxの係数に一致せず、そのような配置または2数の組み合わせでは駄目なことが分かります。そのような場合は、ad+bcの値がxの係数に一致するa，b，c，dがみつかるまで①〜⑥を繰り返し行います。

【アドバイス】

以上で説明を終わりますが、どうでしょう・・分かりましたか？
回答内で挙げた例は、最終的な結果で、そこにたどり着くまでには、何回か①〜⑥を繰り返さなければならないかもしれません・・。ぜひ！自分で試してみてくださいね。そして、駄目なパターンを何回も経験して下さい！それによって、たすきがけの手順にも慣れ、身に付いていきますよ。今後も使う重要な因数分解なので、何回も失敗して上手くなっていきましょう！

では、これからも『進研ゼミ高校講座』を大いに活用し、あなたの学習に役立てて下さいね。