【数列】Σの和の求め方
Σの和の求め方
（1）では 2/1n（n＋1）まではわかるのですが、その後に n をつけるりゆうがわかりません。
（2）も（1）とおなじですが−4n×2/1n（n＋1）−5n の計算のところで、なぜ n がきえたかがわかりません。
進研ゼミからの回答！
こんにちは。
いただいた質問について、早速、回答します。
【質問の確認】
【問題】
次の和を求めよ
の
【解答解説】
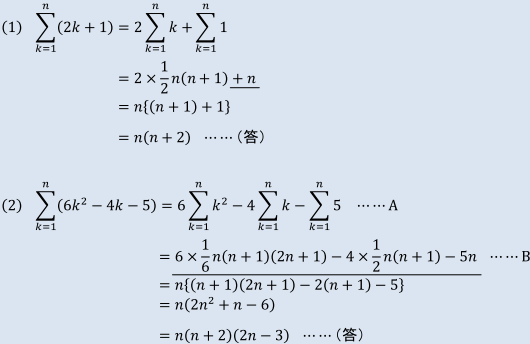
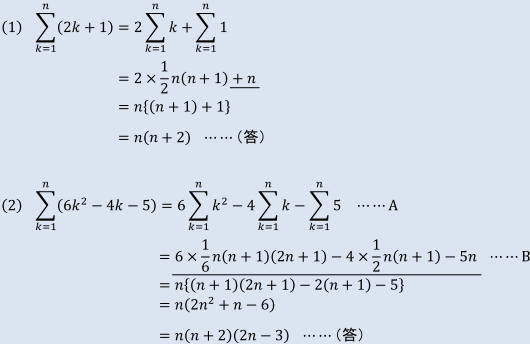
で、「（1）では
まではわかるのですが、その後にnをつけるりゆうがわかりません。
（2）も（1）と同じですが
の計算のところで、なぜnがきえたかがわかりません。」という質問ですね。
【解説】
≪（１）について≫
≪（２）について≫
Ａの式からＢの式への変形は、上に示した和の公式３つを代入したものですね。
ここから先は、このＢの式を整理して、因数の積の形に変形していきます。
つまり、因数分解することになります。Ｂの式には、３つの項がありますが、これらに共通な因数はnですね。そこで、nをくくりだしていきます。
ですから、次の式で、{ }の中はnが消えているのです。
nをくくり出した後は、{ }の中を展開して整理してから、因数分解して（答）を導いています。
【アドバイス】
和の公式はただ覚えるだけでなく、Σの意味を理解しておくと使いこなせるよ
うになります。また、公式を代入してからの式変形は、慣れないと大変ですが、
因数分解すると考えて、共通な数や因数をくくり出していきましょう。
今後も『進研ゼミ高校講座』を活用して得点アップを目指しましょう。
数学のQ&Aランキング
全体のQ&Aランキング
「数列」Q&A一覧
他の教科のQ&Aを見る【その他にも苦手なところはありませんか？】
わからないところをウヤムヤにせず、その場で徹底的につぶすことが苦手を作らないコツ。
「進研ゼミ」には、苦手をつくらない工夫があります。
＜進研ゼミでできること＞授業やテスト前の「わからない」を解消・苦手をつくらない
教科書別に要点をおさえて
予習復習も効率的に！
予習復習 効率UPアプリ
個人のニガテをAIが分析。
力が伸びる問題を自動出題。
AI StLike -個別弱点攻略AI
