【数と式】無理数の整数部分，小数部分の求め方

【質問の確認】

「の整数部分，小数部分を求めなさい。」
という問題で，どうして，3≦＜4という式が出てくるのか，わかりません。
そして，この整数部分が３だと，どうしてわかるのですか？
というご質問ですね。

【解説】

≪整数部分，小数部分の意味≫
例えば，2.236という数では，整数部分は2，小数部分は0.236 となります。

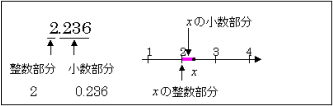
さて，簡単な数の場合，上のように見ればわかりましたが，これを手順として表すと次のようになります。

まず，手順を理解するために，先ほどの2.236を例に，大きな流れをつかみましょう。

手順①　2.236の整数部分を求める。
まず，2.236は，どんな整数の間にある数か，調べます。これを，数直線上に表してみると，

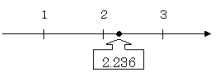
となり，2と3の間にあることがわかりますね。上で示した手順の①の書き方で表すと，2≦2.236＜3となります。
したがって， 2.236の整数部分は2となります。

手順②　小数部分を求める。
「（整数部分）＋（小数部分）＝（もとの数）」ですね。この式を変形して，
「（もとの数）−（整数部分）＝（小数部分）」とすれば，「小数部分」を求めることができますね。
つまり，2.236−2＝0.236となり，小数部分は0.236となります。

これで，手順の概要はつかめましたか？

さて，無理数についても，基本的な考え方は同じです。

手順①　まずn ≦ ＜ n＋1となる整数 nを求める。
の中の数，つまり11が，0²，1²，2²，3²，4²，･･････のどの数の間にあるかを考えます。
（なぜ，(整数)²のように考えるかは後で説明します。）
2² ＝ 4，3² ＝ 9，4² ＝ 16，5² ＝ 25，･･････なので，3² と 4² の間に11があることがわかりますね。
（このように，地道に，11の前後となる，(整数)²を見つけます。）
よって，3² ≦ 11 ＜ 4² と，式にすることができます。
ここで，をつけても大小関係は変わらないので，

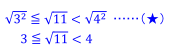
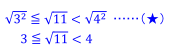
したがって， の整数部分は，３だとわかります。

手順②　小数部分を求める。
（小数部分）＝（もとの数）−（整数部分）なので，小数部分は - 3となります。
よって，答えは， の整数部分は３，小数部分は - 3です。

≪整数部分を考えるときのポイント≫
手順①で，なぜ，(整数)２のように考えたかというと， （★）の計算で，両端に整数が出てくるようにしたためです。
ある数の整数部分を調べるときは，その数が「連続した整数に挟まれる形」にすることがポイントです。

◎オマケ◎
無理数の整数部分，小数部分を求める問題では，
2²，3²，4²，5²，6²，7²，8²，9²，10²，11²，12²，13²，14²，15²
程度の数を覚えておくと，連続した整数を見つけるときに便利ですよ。

【アドバイス】

ある数■の整数部分を調べるときは，■が「連続した整数に挟まれる形」，すなわち，n≦■＜n＋1の形にすることがポイントです。
また，n≦■＜n＋1の形にできたあと整数部分を求めるときに，『n≦■＜n＋1　のとき■の整数部分はn 』ということを丸暗記するのではなく，数直線をかいたり，具体的な数で考えたりして，導けるようにしておくことで，ケアレスミスを防げるでしょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。