【数と式】たすきがけはいつ使うのか
たすきがけはいつ使うのか
解答解説&講義を見ると、式の途中にたすきがけが使われていますが、あれはいつ、どのような式が出た時にやればよいのですか?
また、解説の★の部分がなぜあの式になるのか分かりません。
進研ゼミからの回答!
こんにちは。
いただいた質問について、早速、回答します。
【質問の確認】
● たすきがけのタイミングと、
【問題】
次の式を因数分解せよ。
3x2 + xy - 2y2 + 6x + y + 3
について
【解答解説】
3x2 + xy - 2y2 + 6x + y + 3
= 3x2 + (y + 6)x - 2y2 + y + 3
= 3x2 + (y + 6)x - (2y2 - y - 3)


= 3x2 + (y + 6)x - (2y - 3)(y + 1) ・・・★
= {3x - (2y - 3)}{x + (y + 1)} ・・・★
= (3x - 2y + 3)(x + y + 1) ・・・・・・(答)
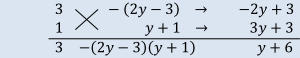
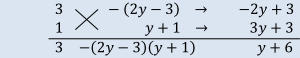
の★の式変形部分について、ですね。
【解説】
≪たすきがけのタイミング≫
因数分解は、式の展開と逆の変形ですね。
よって、○x2 + △x + □ のタイプの式の因数分解は、
![]()
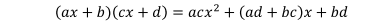
に当てはめて考えるのですが、たとえば、5x2 - 11x + 2 を見ても、すぐにa、b、c、dの値がわかりません。これらの値を簡単に求めるためのテクニックとして「たすきがけ」があります。
つまり、たすきがけは ○x2 + △x + □ のタイプの式の因数分解を考えるときに利用します。


今回の問題のように、xとyの2つの文字を含むときは、x、yのどちらかに注目します。
xに注目して、


《たすきがけの仕方》
たすきがけの因数分解
acx2 + (ad + bc)x + bd
= (ax + b)(cx + d)
![]()
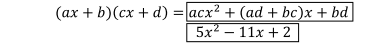
これらを見比べると、aとcは掛けると5となる、bとdは掛けると2となる数字であるから、ac = 5,bd = 2 を満たすa、b、c、dを考え、その中からad + bc = -11 となる組み合わせを求めればよいことがわかりますね。
ac = 5,bd = 2 を満たすaとc、bとdの候補をa = 5,c = 1 と b = 2, d = 1と考えた場合は、次のように書きます。


次に、斜めにある数字aとd、bとcを掛けて右に書くと、 adとbcを求めたことになります。
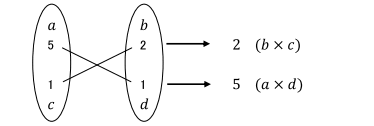

この2つの数字を足すと、ad + bc を求めた事になるので、この場合は7となります。
adとbcの2つの数の和がxの係数(−11)となる場合を求めるのだから、これは不適当であることがわかります。aとd、bとcの値を変えて、ad + bc = −11 となる場合を考えると


とすると、ad + bc = −11 となりますね。
このようにして、a、b、c、dの値を求めます。慣れるまでは、展開の公式を見ながら考えるとわかりやすいですよ。
《★の式変形について》
さて、今回与えられた式は、xとyの2つの文字が含まれているので複雑な式と感じられるかもしれません。このような式は、どちらか1つの文字についての式と考えることが大切です。
ここでは、
・xについての式と考えて、xについて降べきの順に整理
・xを含まない部分を因数分解
と考えて変形していきます。
まず、xについて降べきの順に整理して、
![]()
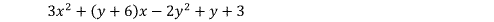
となり、xを含まない部分を因数分解することを考えます。
-2y2 + y + 3 = -(2y2 - y - 3) と変形すると、カッコの中は、○y2 + △y + □ の形をしているので、たすきがけをして因数分解をします。
すると、2y2 - y - 3 = (2y - 3)(y + 1) と変形できますね。
これより、3x2 + (y + 6)x - 2y2 + y + 3 = 3x2 + (y + 6)x - (2y - 3)(y + 1) となります。
この式は、○x2 + △x + □ の形をしているので、たすきがけを利用しましょう。
文字が2つあるので難しく感じるかもしれませんが、yは定数として ○x2 + △x + □ のタイプと同じように考えましょう。
つまり、掛けると3(x2 の係数)となる2つの数と、掛けると定数項 −(2y - 3)(y + 1)になる2つの式を考えて、たすきがけをするので、
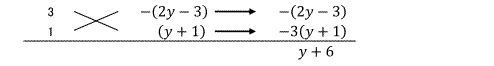
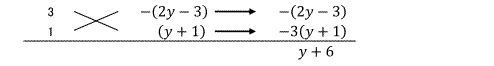
となりますね。
よって、
![]()
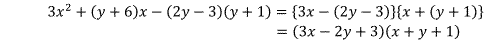
と導けるのです。
【アドバイス】
複雑な式を扱うときも考え方は基本の因数分解と同じなので、どのパターンにあてはめられるかを考えて、パターンに沿って考えるようにするとわかりやすいですよ。
今後も『進研ゼミ高校講座』を使って、積極的に学習を進めてください。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「数と式」Q&A一覧
「数と式」Q&A一覧
- 【数と式】「pならばq 」が真のとき,集合Pが集合Qに含まれる理由
- 【数と式】たすきがけのやり方について
- 【数と式】たすきがけはいつ使うのか
- 【数と式】ルートの中が「負の数の2乗」のときの,ルートのはずし方
- 【数と式】因数分解のしかた
- 【数と式】因数分解の式の整理について
- 【数と式】因数分解の式変形について
- 【数と式】因数分解をするときの途中式について
- 【数と式】対称式はどんなとき使うんですか?
- 【数と式】式変形するときの文字の置き換え方
- 【数と式】必要条件・十分条件
- 【数と式】文字を含む式の書き方
- 【数と式】無理数の整数部分,小数部分の求め方
- 【数と式】絶対値と場合分け
- 【数と式】絶対値記号の意味
- 【数と式】絶対値記号を含む方程式・不等式の解き方
- 【数と式】負の値の絶対値の考え方について
- 【数と式】逆・裏・対偶の関係
- 【数と式】連立不等式の解の求め方
- 【数と式】2重根号の計算












