有理数ってどんな数?
有理数ってどんな数?分数で表せる数の見分け方と無理数との違いが知りたい
有理数とは、分数で表すことができる数のことです。
有理数とは、分数で表すことができる数のことです。
数式で表すと次のようになります。
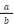
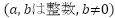
この形で表せる数をすべて「有理数」と呼びます。
-
整数も有理数
例: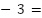
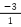 、
、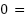
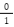 、
、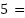
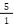
-
分数も有理数
例: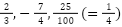
つまり、整数・分数・0 をすべてまとめた数の集まりが有理数なのです。
有理数の分類と小数表示
有理数は「分数で表せる数」ですが、見た目の形はさまざまです。整数として書ける場合もあれば、小数で表される場合もあります。ここでは、有理数を 整数・有限小数・循環小数 に分けて整理し、さらに「小数表示から有理数かどうかを見分ける方法」について確認していきましょう。
有理数の分類(整数・有限小数・循環小数)
有理数には、次のようにいくつかの表し方があります。
-
整数:分母を 1 とすれば分数で表せる
例:-2,0,7 -
有限小数:小数が有限の桁で止まる数(=分数に直せる)
例: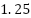 =
= 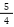 、
、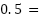
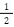
-
循環小数:同じ数字の並びが繰り返し現れる数(=分数に直せる)
例: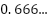 =
= 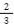 、
、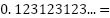
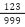
| 分類 | 例 |
|---|---|
| 整数 | -2,0,7 |
| 有限小数 | 1.25 = 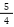 , 0.5 = , 0.5 = 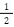 |
| 循環小数 | 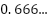 = = 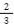 、 、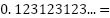 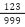 |
一方で、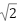 のように分数で表せない数は「無理数」に分類されます。
のように分数で表せない数は「無理数」に分類されます。
例題
次の数のうち、有理数をすべて選びましょう。
① -2 ② 1.25 ③ 0.666... ④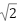
解答
① -2(整数)
② 1.25(有限小数=分数に直せる)
③ 0.666...(循環小数=分数に直せる)
④ 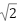 (分数に直せないので無理数)
(分数に直せないので無理数)
よって、有理数は ①②③ です。
有理数の小数表示と見分け方
有理数を小数で表すと、必ず 「有限小数」または「循環小数」 になります。逆に、小数が止まらず、しかも繰り返しのない数は無理数です。
見分け方のポイント
-
小数が有限で終わる → 有理数
例:0.25 =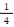 、1.5 =
、1.5 = 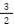
-
小数が無限に続くが、同じ並びが繰り返す(循環小数) → 有理数
例:0.333...=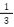 、0.142857142857...=
、0.142857142857...= 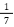
-
小数が無限に続き、しかも繰り返しがない → 無理数
例:π = 3.14159265...、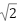 = 1.41421356...
= 1.41421356...
例題
問題
0.123123123... は有理数でしょうか?
解答
はい。有理数です。小数点以下が「123」の並びを繰り返しているので 循環小数 です。実際に分数に直すと、
0.123123123... = 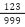
となり、分数の形で表せます。
このように、「止まるか繰り返すか」を見ると、有理数かどうかをすぐに判断できます。
無理数との違い
有理数とよく比較されるのが「無理数」です。有理数が「分数で表せる数」であるのに対して、無理数は分数で表すことができない数です。ここからは、無理数の定義や具体例を見て、有理数との違いを整理しましょう。
無理数とは?
無理数とは、整数分の整数(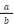 の形)で表せない数のことです。
の形)で表せない数のことです。
小数で表すと 止まらず、繰り返しのない並びが続きます。
- 代表的な無理数
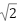 = 1.41421356...(止まらない・繰り返さない)
= 1.41421356...(止まらない・繰り返さない)- π = 3.14159265...(円周率、無限に続く)
- e = 2.7182818...(自然対数の底)
一方、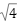 = 2のように、整数として表せる場合は「有理数」に分類されます。
= 2のように、整数として表せる場合は「有理数」に分類されます。
| 分類 | 具体例 | 小数表示 |
|---|---|---|
| 有理数 | 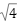 = 2 = 2 |
2.0(有限小数) |
| 有理数 | 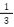 |
0.333...(循環小数) |
| 無理数 | 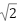 |
1.41421356...(非循環) |
| 無理数 | π | 3.14159265...(非循環) |
よくある判定ミスに注意しよう
有理数と無理数を判定するとき、高校生がよく間違えるケースがあります。ここでは代表的な誤りを整理しておきましょう。
-
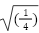 は有理数
は有理数
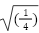 =
= 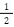 なので、分数で表せます。
なので、分数で表せます。
-
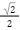 は無理数
は無理数
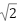 が無理数なので、その倍数や分数も無理数のままです。
が無理数なので、その倍数や分数も無理数のままです。
-
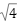 は有理数
は有理数
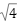 = 2 と整数で表せるため、有理数です。
= 2 と整数で表せるため、有理数です。
このように「ルートがついているから全部無理数」と考えるのは間違いです。計算して分数や整数になれば有理数と判断できます。
【判定ミスをしないためのチェック手順】
- 1.まず√の中身を確認:完全平方(または分子分母が平方)か
- 2.√から外へ出せるものは外へ:
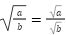
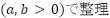
- 3.√が消えれば有理数/消えなければ無理数
有理数の集合としての性質
有理数は「分数で表せる数」というだけでなく、数の世界を整理するうえで重要な位置づけを持っています。ここでは、有理数を「集合」としてとらえ、記号や他の集合との関係を確認していきましょう。
有理数の集合と記号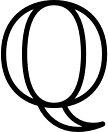
有理数の全体をまとめた集合は、次のように書きます。
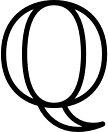
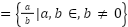
ここで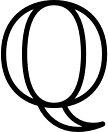 という記号は、Quotient(商) の頭文字に由来しています。「分数=割り算=商」というイメージを反映したものです。
という記号は、Quotient(商) の頭文字に由来しています。「分数=割り算=商」というイメージを反映したものです。
他の集合との関係を整理すると次のようになります。
- 自然数(
 ):1,2,3...
):1,2,3... - 整数(
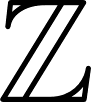 ):...,-2,-1,0,1,2,...
):...,-2,-1,0,1,2,... - 有理数(
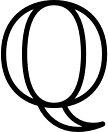 ):整数や分数、有限小数・循環小数を含む
):整数や分数、有限小数・循環小数を含む - 実数(
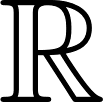 ):有理数+無理数
):有理数+無理数
つまり、
 ⊂
⊂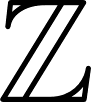 ⊂
⊂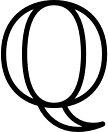 ⊂
⊂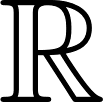
という包含関係になっています。
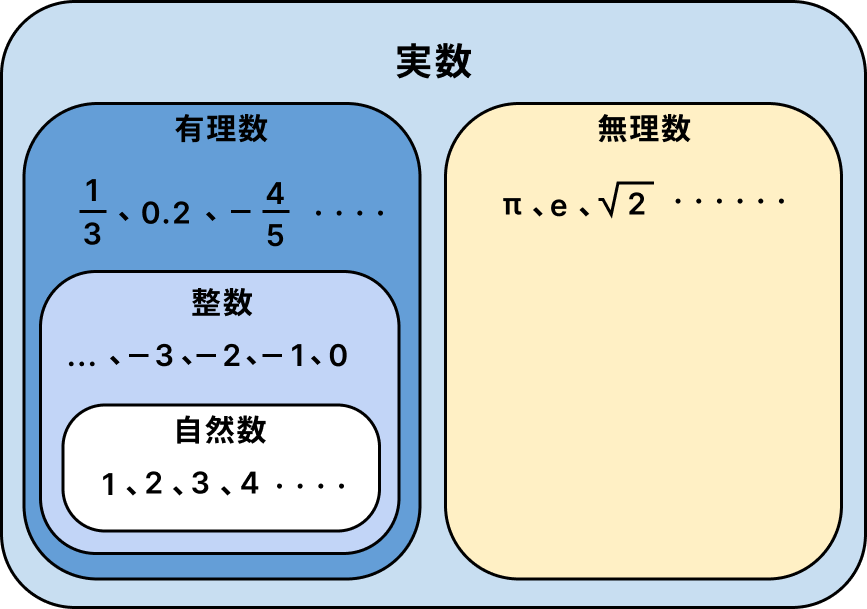
実数の分類図。実数は有理数と無理数に分かれ、有理数には整数や自然数が含まれる。例: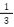
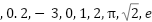
有理数の演算の性質
有理数の大きな特徴は、四則演算(足し算・引き算・掛け算・割り算)に強いことです。
1. 演算に「閉じている」
有理数どうしで加減乗除を行うと、結果も必ず有理数になります。 ただし、割り算のとき 0 で割ることだけはできないので注意しましょう。
- 加法:
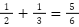 (有理数)
(有理数) - 減法:
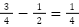 (有理数)
(有理数) - 乗法:
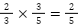 (有理数)
(有理数) -
除法:
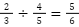 (有理数)
(有理数)
※ただし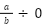 は未定義
は未定義
2. 性質をまとめると
- 足し算・引き算・掛け算・割り算(0除く) → 結果は有理数
- このことを「有理数は四則演算に関して閉じている」といいます
例題
次の計算結果は有理数かどうか答えましょう。
① 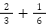
② 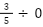
解答
① 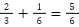 → 有理数
→ 有理数
② 0 で割っているため計算できない → 有理数ですらない
「0で割る場合」を除けば、どんな計算でも有理数に収まるのが大きな特徴です。
有理数の使い方をケース別に紹介(実生活・入試・応用)
有理数は教科書上の知識だけでなく、私たちの生活や入試問題、そして数学の応用分野でも広く登場します。ここでは、実生活 → 入試 → 応用と段階的に見ていきましょう。
実生活における有理数
実は日常生活の中で、私たちは無意識のうちに有理数を使っています。身近な例を見てみましょう。
-
割り勘
3人で 1500 円を割り勘すると、1人あたり 1500 ÷ 3 = 500 円。これは整数=有理数です。 -
時間の表し方
1 時間半を「1.5 時間」と表すと、これは有限小数=有理数です。 -
商品の価格
ガソリンが 1ℓ あたり 168.7 円なら、小数で表された値段ですが、これも有限小数=有理数です。
このように、お金の計算・時間の表現・数量の扱いなど、私たちの生活は有理数に支えられています。
入試での有理数の出題例
有理数は中学〜高校初期にかけての基礎単元なので、共通テストや定期試験でも頻出です。特に「定義」「小数での見分け方」「平方根を含む式の判定」などがよく問われます。
典型的な問題例
問題
次のうち、有理数でないものを選びなさい。
① 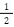 ②
② 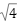 ③
③ 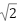 ④ 0.25
④ 0.25
解答
- ①
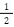 = 分数 → 有理数
= 分数 → 有理数 - ②
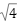 = 2(整数) → 有理数
= 2(整数) → 有理数 - ③
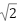 = 1.41421356...(分数で表せない) → 無理数
= 1.41421356...(分数で表せない) → 無理数 - ④ 0.25 =
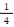 (有限小数) → 有理数
(有限小数) → 有理数
よって答えは ③ 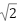 です。
です。
出題のポイント
- 定義の理解:「分数で表せるかどうか」が基本
- 小数表示の判定:「止まる/繰り返す」なら有理数
- 平方根の扱い:計算して整数・分数になれば有理数、そうでなければ無理数
数学的・応用的な有理数の使い道
有理数は「分数で表せる数」としての理解にとどまらず、数学のさまざまな分野で基盤となる道具として活用されます。
応用シーンの例
-
確率
サイコロを振って「1の目が出る確率」は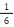 。 分数として表現できるので有理数です。
。 分数として表現できるので有理数です。
-
平均値の計算
テストの得点を合計して人数で割った値は、多くの場合有限小数。これも有理数です。 -
式変形や関数の係数
例: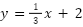 のように、文字式の係数として有理数が頻出します。(無理数の場合もある)
のように、文字式の係数として有理数が頻出します。(無理数の場合もある)
有理数の強み
無理数(πや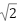 )は近似値でしか扱えませんが、有理数は 正確に値が決まる という利点があります。そのため、計算の基準・道具として数学の土台になっているのです。
)は近似値でしか扱えませんが、有理数は 正確に値が決まる という利点があります。そのため、計算の基準・道具として数学の土台になっているのです。
まとめ|有理数の意味と大事なポイント
有理数は「分数で表せる数」のこと
→ 整数・分数・有限小数・循環小数をすべて含む。
小数表示で見分けられる
→ 止まる(有限小数)か、繰り返す(循環小数)なら有理数。
→ 止まらず繰り返しのない小数は無理数。
無理数との違いを押さえる
→ 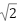 やπのように分数で表せない数は無理数。
やπのように分数で表せない数は無理数。
→ 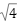 = 2 のように計算して整数になれば有理数。
= 2 のように計算して整数になれば有理数。
有理数は集合として重要
→ 自然数 ⊂ 整数 ⊂ 有理数 ⊂ 実数 という階層の一部をなす。
→ 四則演算(0で割る場合を除く)に閉じているのも特徴。
生活や入試でよく登場
→ 割り勘・時間・価格表示など日常生活に直結。
→ 定期テストや入試では「定義の理解」「小数からの判定」「平方根の扱い」で頻出。
ただ実際の学習では、
- √がついていると全部「無理数」だと思ってしまう
- 有限小数や循環小数を分数に直す方法があいまい
- 0で割るケースに気づかず誤答する
といった壁に直面する高校生は多いです。そんなときに役立つのが 進研ゼミのAI質問機能(お試し無料)。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「数と式」Q&A一覧
「数と式」Q&A一覧
- 【数と式】「pならばq 」が真のとき,集合Pが集合Qに含まれる理由
- 【数と式】たすきがけのやり方について
- 【数と式】たすきがけはいつ使うのか
- 【数と式】ルートの中が「負の数の2乗」のときの,ルートのはずし方
- 【数と式】因数分解のしかた
- 【数と式】因数分解の式の整理について
- 【数と式】因数分解の式変形について
- 【数と式】因数分解をするときの途中式について
- 【数と式】対称式はどんなとき使うんですか?
- 【数と式】式変形するときの文字の置き換え方
- 【数と式】必要条件・十分条件
- 【数と式】文字を含む式の書き方
- 【数と式】無理数の整数部分,小数部分の求め方
- 【数と式】絶対値と場合分け
- 【数と式】絶対値記号の意味
- 【数と式】絶対値記号を含む方程式・不等式の解き方
- 【数と式】負の値の絶対値の考え方について
- 【数と式】逆・裏・対偶の関係
- 【数と式】連立不等式の解の求め方
- 【数と式】2重根号の計算
- 【数と式】有理数ってどんな数?分数で表せる数の見分け方と無理数との違いが知りたい
- 【数と式】無理数ってどんな数?有理数との違いや身近な例も知りたい














