確率計算の公式は覚えているけど、どこで使うか分からない

確率計算の方法

確率の学習でまず押さえておきたいのは「公式の整理」です。公式自体はシンプルですが、使う場面を理解していないとテストで混乱します。

ここでは、定期テスト・入試で必ず出る公式を一覧にしました。暗記ではなく「使い分け」を意識しましょう。

確率の定義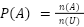
和の法則	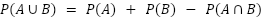A,Bが排反事象の場合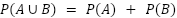
独立事象の確率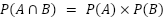
余事象の確率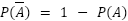
条件付き確率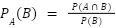

覚えておくべき使い分け

確率の公式はシンプルですが、実際の問題では「どの公式を選ぶか」で迷いがちです。そこでまずは、典型的な使い分けを整理しておきましょう。

このように、問題文のキーワードに反応できると、公式の選び方で迷わなくなります。

ポイント解説

ただ公式を丸暗記するだけでは、本番で十分に使いこなせません。大切なのは、公式を「どの場面で使うのか」と結びつけて覚えることです。

たとえば、

さらに、図解とセットで覚えると理解が一気に深まります。和の法則はベン図で「重なり」を描いて確認、積の法則は樹形図で「枝の組合せ」を整理、条件付き確率はベン図で部分集合をイメージすると、公式の意味が直感的にわかります。

最後に、練習では必ず「この問題はどの公式を使うのか？」を声に出して確認するのがおすすめです。典型的な言葉のサインを見抜けるようになると、定期テストでも入試でも素早く正しい公式を選べるようになります。

場合の数と確率の関係

確率の問題を解くとき、最も大切なのは「全体のパターン数」と「注目する事象の数」を正しく数えることです。そのために必要になるのが場合の数です。

順列と組合せの整理

順列と組み合わせは似ているようで全く違うもの。使い分けを間違えると、確率計算の最初の段階でつまずいてしまいます。

項目	記号	計算式	使う場面
順列		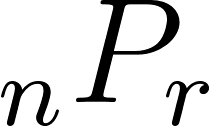	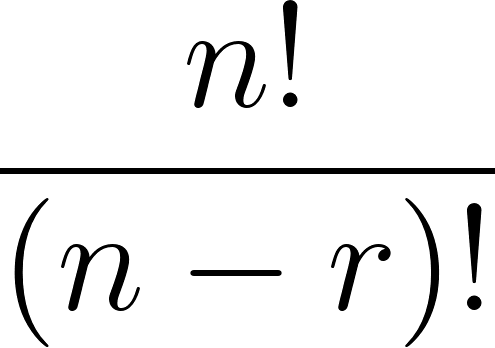順番を区別するとき
組合せ		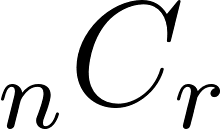	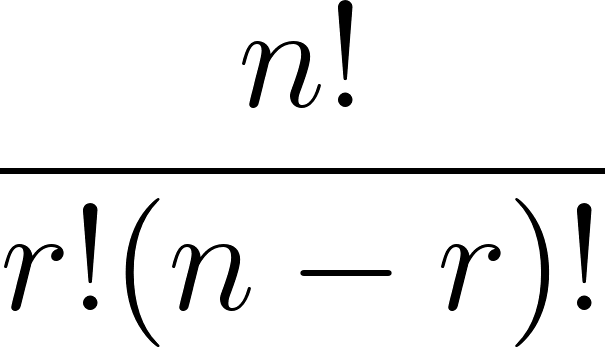順番を区別しないとき

確率を求めるときは、以下の手順を徹底しましょう。

1. 全体のパターン数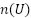を数える

• サイコロ2個 → 6 × 6 = 36通り
• 5枚から2枚選ぶ → ₅C₂ = 10通り

2. 注目する事象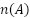を数える

• 条件に合うパターンを順列や組合せで数える

3. 確率を計算する

• 

樹形図・ベン図を用いた基本問題

確率の計算でつまずく原因のひとつが「数え漏れ」や「同じものを2回数えてしまう」ことです。これを防ぐには樹形図やベン図を使って、目に見える形で整理するのがおすすめです。

例題1：サイコロ2個の合計が7になる確率を求めなさい。

全体のパターン数は 6×6 = 36

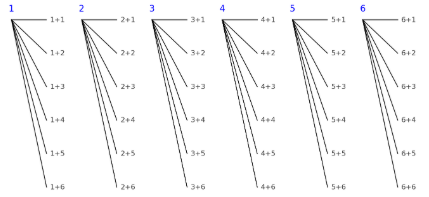
樹形図を描くと、最初のサイコロの出目ごとに6通りの枝が伸び、合計36パターンが確認できます。和が7になる組み合わせは

(1,6), (2,5), (3,4), (4,3), (5,2), (6,1) の6通りです。

よって求める確率は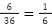となります。

例題2：赤玉3個・青玉2個の袋から2個同時に取り出すとき、赤玉2個を引く確率を求めなさい。

全体の組合せ→5個から2個を選ぶ → ₅C₂ = 10通り

赤玉2個を選ぶ場合

赤3個から2個を選ぶ → ₃C₂ = 3通り

よって求める確率は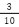です。

応用問題

例題3：コインを3回投げて表が2回出る確率を求めなさい。

解答

ステップ1：全体の事象数
コイン1回につき表・裏の2通り → 3回投げると 2³ = 8通り

ステップ2：条件に合う場合の数
表が2回出る並び方は

表表裏
表裏表
裏表表 の3通り

ステップ3：確率を計算
求める確率は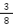

補足： 反復試行の確率

3回のうち2回が表、1回は裏 →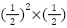

表が何回目に出るか→1回目、2回目、3回目の内2回なので₃C₂ = 3通り

求める確率は

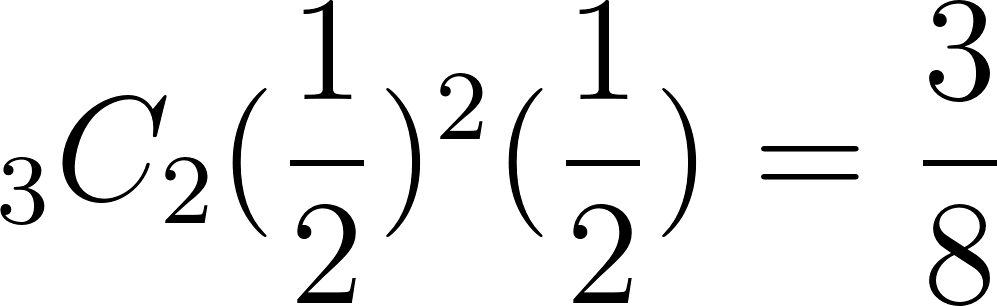
例題4：ジョーカーを除くトランプ52枚から1枚を引いてハートかスペードが出る確率を求めなさい。

解答

ステップ1：全体の事象数

• 52枚

ステップ2：条件に合うカード

• ハート：13枚
• スペード：13枚
• 重なりはなし

ステップ3：確率を計算

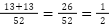
例題5：サイコロで偶数が出たとき、2の目が出る確率を求めなさい

ステップ1：条件付き確率の定義

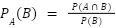
ステップ2：事象を整理

• B：偶数（2,4,6） → 3通り(これが分母となる)
• A：2の目 → 1通り
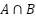• ：同時に満たすもの → 2（1通り）

ステップ3：確率を計算

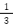
ポイントは全体の6通りではなく、条件に合う3通りを分母にすることです。 条件付き確率では、母集団が変わる点に注意しましょう。

テストでよくある落とし穴

確率の公式や場合の数を理解していても、テスト本番では思わぬところで失点することがあります。ここでは高校生が特につまずきやすいポイントを整理しました。

① 順列と組合せの混同

• ミス例：「3人から2人を選ぶ」を順列で計算してしまう
• 対策：「順番を区別するかどうか」で必ず判断する

② 分母の取り違え（条件付き確率）

• ミス例：サイコロで「偶数が出たとき」と言われても、全体6通りを分母にしてしまう
• 対策：「条件に合う範囲が新しい全体になる」と意識する

③ 余事象の使い忘れ

• ミス例：複雑な場合分けをすべて数えようとして時間切れになる
• 対策：「〜でない確率」は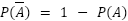を思い出す

④ 数え漏れ・数え重複

• ミス例：樹形図や表を描かずに頭だけで処理して抜けが出る
• 対策：簡単な図を書いて整理するクセをつける

⑤ 全体のパターン数を勘違い

• ミス例：サイコロ2個の全体を「6通り」と思い込む
• 対策：全体は掛け算で数える（6×6=36通り）ことを忘れない

まとめ｜確率計算のやり方と大事なポイント

確率は「起こる場合の数 ÷ 全体の数」
→ すべての公式・解法の出発点となる基本。

公式の整理を押さえる
→ 和の法則・積の法則・余事象・条件付き確率を使い分ける。

場合の数とセットで考える
→ 順列・組合せを正しく使い分け、全体と事象を正確に数える。

図で整理する習慣をつける
→樹形図やベン図を描くと「数え漏れ・重複」が防げる。

典型問題で練習して定着させる
→ サイコロ・コイン・カードのような基本問題は入試まで繰り返し練習する。

ただ実際の学習では、

• どの公式を選べばいいか迷う
• 分母を間違えてしまう（条件付き確率）
• 場合分けが複雑になりすぎる
• 図を描かずに処理して数え漏れする

といった壁に直面する高校生は多いです。そんなときに役立つのが進研ゼミのAI質問機能（お試し無料）。

AI質問の特徴

問題を撮影するだけ！
勉強中にわからない数学の問題を撮影すると、すぐにヒントや解き方を丁寧に解説してくれます。

考え方や途中過程まで、ステップごとに解説
答えだけでなく、解答に至るまでのステップをわかりやすく提示。追加解説まで丁寧に説明してくれます。

AI質問機能を活用することで、定期テストや入試の対策に向けて、理解の“穴”をすぐに埋めることに役立ちます。「進研ゼミ」は以下よりダウンロードください。