【図形と計量】余弦定理の基本と使い方を例題で解説

余弦定理とは？

ではまず、余弦定理とは何か？からご説明しますね。 余弦定理は、三角形の辺の長さと角の大きさの関係を表す便利な公式です。

どんな時に使うの？

余弦定理は、主に次の 2 つの場合に役立ちます。

余弦定理の公式はこれ！

三角形の 3 つの角を A, B, C、それぞれの角の向かいにある辺の長さを a, b, c とします。

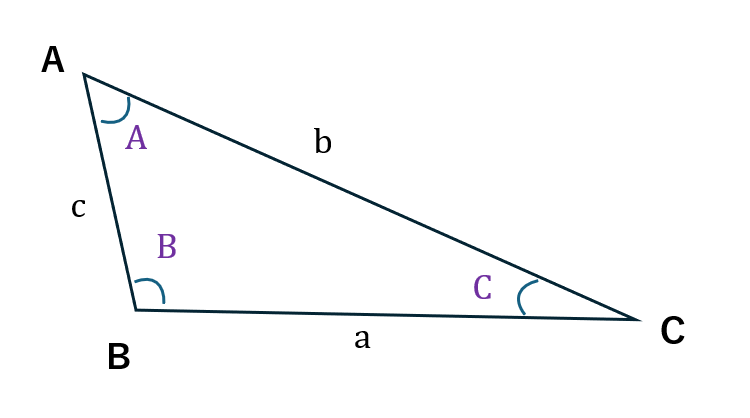
このとき、余弦定理は次の 3 つの式で表されます。

「え、3 つも覚えるの？」って思うかもしれませんが、実は全部同じ形をしていて、文字が変わっているだけなんです。

代入のしかたを具体的に見てみよう

例題１：3辺の長さから、cosAを求める
三角形 ABC で、a=13，b=7，c=15 のとき、cosAを求めてみましょう。

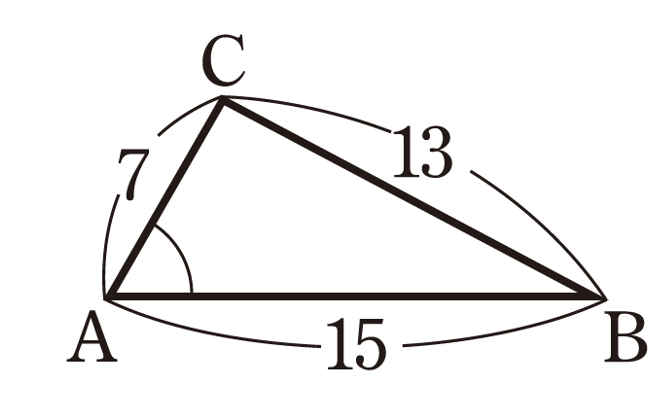
【解答】

１．どの公式を使うか決める
cosA を求めたいので、a² = b² + c² - 2bc cosA の式を使います。

２．値を代入する
a² = 13² = 169
b² = 7² = 49
c² = 15² = 225
2bc = 2×7×15 = 210
式に代入すると、169= 49 + 225 - 210 cosA となります。

３．cosA について解く
169 = 274 – 210 cosA
210 cosA =105
cosA = 105 ÷ 210 = 1/2

例題2：2辺の長さとその間の角から残りの辺の長さを求める
三角形 ABC で、a = 5, b = 3, C = 60° のとき、辺 c の長さを求めたいとします。

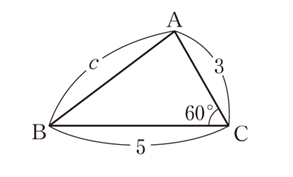
【解答】

１．どの公式を使うか決める
わかっている a，b，C は 2辺とその間の角の関係なので，余弦定理を使います。辺 c を求めたいので、c² = a² + b² - 2ab cosC の式を使います。

２．値を代入する
a² = 5² = 25
b² = 3² = 9
2ab = 2 ×5 × 3 = 30
cosC = cos60°= 1/2
式に代入すると、c² = 25 + 9 - 30 × (1/2) となります。

３．c²を計算する：
c² = 25 + 9 - 15 = 19

４．c を求める
c＞0 だから
c = √19

代入するときの注意点

●図をかいて、求めたい辺や角の位置関係を把握する！
辺と角の位置関係をつかむための図をかきます。
・辺の長さ，角の大きさは正確にかかなくても大丈夫。だいたいの角の大きさや、辺の長さのどちらが長いのかなど、わかっている情報を使ってかいてみよう。
・角と辺の対応関係を間違えないように注意しよう。

たとえば、△ABCが、a=1+√3、ｃ=√２、B=45° の場合、




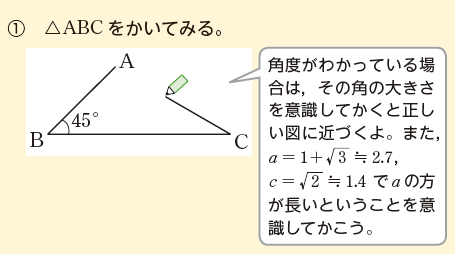
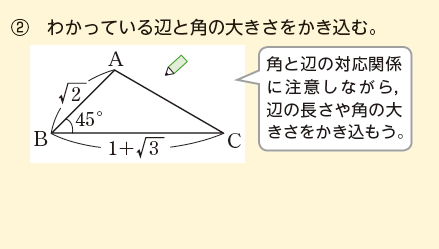
●どの角と辺の関係か、しっかり確認する
公式の a, b, c, A, B, C が、問題の図でどの部分に対応しているか、間違えないようにしましょう。

●よく使う cos の値は覚えておくと便利
これだけは覚えておくとよいでしょう。


●計算ミスに気を付ける
特に、符号の間違いに注意しましょう。