【2次関数】2次関数とは？基本から解説

2次関数とは？

高校数学で重要な「2次関数」。グラフの形や特徴を理解することで、最大値や最小値を求めたり、さまざまな問題を解くための強力な武器になります。
2次関数とは、次のような式で表される関数のことです

y = ax ² + bx + c (a ≠ 0)

この式で、xの値が決まると、yの値も一つに決まります。この対応関係を表したものが2次関数です。

2次関数のグラフは放物線

2次関数のグラフは、放物線というU字型の曲線になります。放物線の形は、係数 a の値によって変わります。

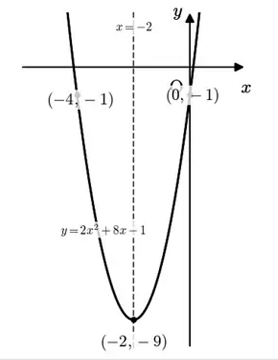
a＞0のとき：下に凸

y = 2x² + 8x -1の場合

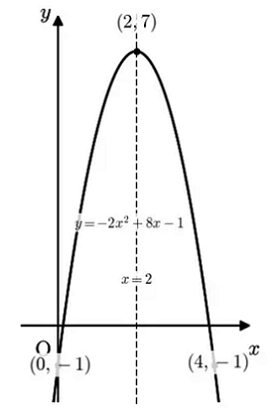
a＜0のとき：上に凸

y =－2x² + 8x -1の場合

グラフの頂点と軸

放物線には、頂点と軸という重要な要素があります。

頂点→（p,q）

軸→x=p

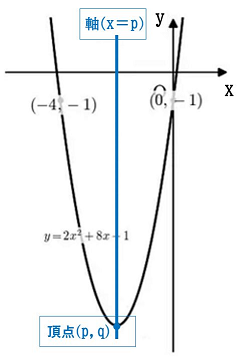
頂点の座標は、2次関数の式を変形することで求めることができます。

平方完成とは、頂点を見つける魔法

2次関数の式 y = ax² + bx + c のままでは、頂点の座標がわかりにくいです。そこで、平方完成というテクニックを使って、式を変形します。

平方完成とは、式を y = a(x - p) ² + q の形に変形することです。この形に変形すると、
・頂点の座標： (p, q)
・軸の方程式： x = p
を求めることができます。

平方完成のやり方

例として、y = x² + 4x + 3 を平方完成してみましょう。
1. x² + 4x の部分に注目し、(x + 2)² を作ります。(x + 2)² = x² + 4x + 4 なので、元の式と合わせるために、余分な +4 を引きます。
2. y = (x + 2)² - 4 + 3
3. y = (x + 2)² - 1
これで平方完成できました！この式から、頂点の座標は (-2, -1)、軸の方程式は x = -2 であることがわかります。

例題：平方完成を使って、頂点と軸を求めてみよう！

2次関数y = 2x² + 8x - 1 の、頂点と軸を求めて、グラフをかいてみましょう。

【解答】

最大値と最小値

二次関数には、最大値または最小値が存在します。

•下に凸の放物線： 頂点で最小値をとり、最大値はなし
•上に凸の放物線： 頂点で最大値をとり、最小値はなし

ただし、定義域（xの範囲）が制限されている場合は、最大値または最小値が存在しない場合や、頂点以外の場所で最大値・最小値をとる場合もあります。

例題：最大値・最小値を求めてみよう！

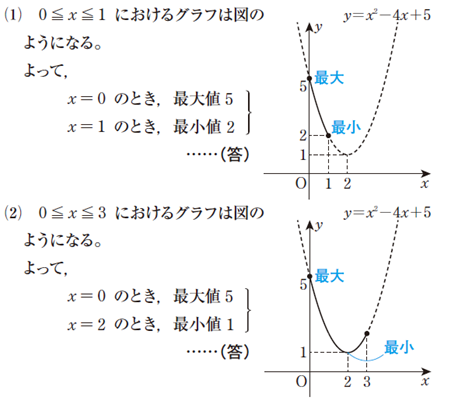
次の定義域において，2次関数 y=x²-4x+5 の最大値，最小値を求めよ。

(1) 0≦ｘ≦1
(2) 0≦ｘ≦3

解説

まず平方完成して、頂点の座標を求めましょう。

ｙ = x² - 4x + 5
= x² - 4x + 2² - 2² + 5
= (x - 2)² +1

頂点（2,1）