正弦定理の基本と使い方を例題でマスター

正弦定理とは

正弦定理の基本と使い方について、例題を使いながらご説明しますね。
正弦定理は、三角形の辺の長さと角のサイン（sin）の間に成り立つ便利な定理です。具体的には、以下のようになります。

三角形ABCにおいて、各辺の長さをそれぞれa, b, cとし、それぞれの辺の対角の大きさをA, B, Cとすると、

a / sinA = b / sinB = c / sinC = 2R

が成り立ちます。ここで、Rは三角形ABCの外接円の半径です。

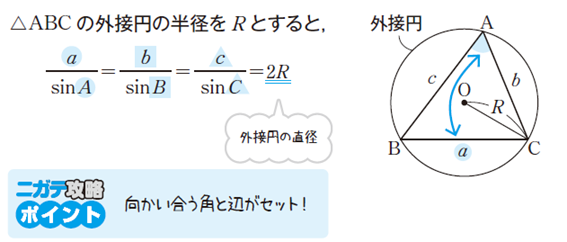
つまり、
・(辺の長さ) / (その対角のサイン) は、どの辺と角の組み合わせでも一定の値になる
・その値は、外接円の直径に等しい
ということです。

正弦定理は、どんなときに使える？

正弦定理は、主に以下の３つの場合に使えます。

1.三角形の辺の長さを求める
・2つの角の大きさと、1つの辺の長さがわかっているとき

2.三角形の角の大きさを求める
・2つの辺の長さと、1つの対角の大きさがわかっているとき

3.三角形の外接円の半径を求める
・辺の長さと、その対角の大きさが１組わかっているとき

正弦定理の使い方を例題で確認

では実際に正弦定理を使って例題を解いてみましょう。

例題1：辺の長さを求める

三角形ABCにおいて、b= 2，∠B = 45°, ∠C = 60 °のとき、辺cの長さを求めよ。

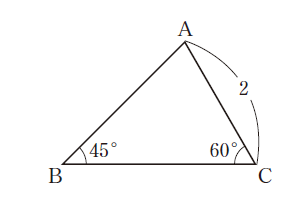
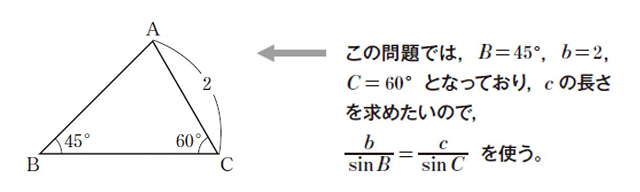
考え方
・わかっている情報：2つの角（∠B, ∠C）と1つの辺（b）
・求めたいもの：辺ｃの長さ
・使う定理：正弦定理

解答

正弦定理より、

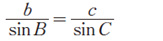
ここに、わかっている値を代入します。

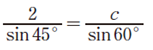
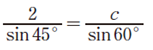
両辺にsin60°をかけます。

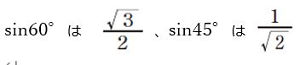
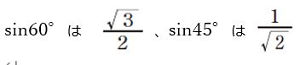
なので、

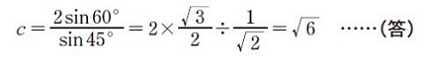
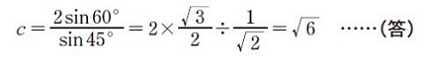
したがって、辺cの長さは√6です。

ポイント
• 正弦定理を使う際は、どの辺と角の組み合わせを使うかを見極めることが重要です。

例題2：１つの辺と、外接円の半径を求める

三角形ABCにおいて、a = 8, ∠A = 30°, ∠C = 135°のとき、cと外接円の半径Ｒの大きさを求めなさい。

考え方
・わかっている情報：2つの角（∠A, ∠C）と1つの辺（a）
・求めたいもの：ｃ、外接円の半径R
・使う定理：正弦定理

解答

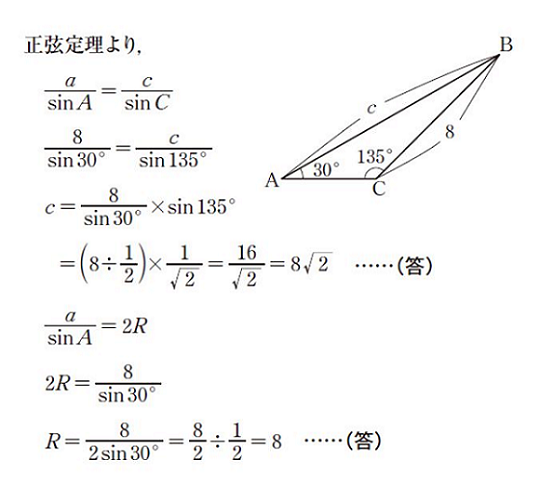
まとめ

正弦定理は、三角形の辺の長さと角のサインを結びつける便利な公式です。
・(辺の長さ) / (その対角のサイン) = 2R（外接円の直径）
この関係を理解し、例題を通して使い方をマスターすることで、さまざまな三角形の問題を解くことができるようになります。
分母と分子の対応に注意しながら、正弦定理を使いこなしましょう！