【図形と計量】正弦定理と余弦定理のどっちを使えばいいんですか?
正弦定理と余弦定理のどっちを使えばいいんですか?
この問題でも、解答解説1行目で「余弦定理より」とはじまっているのですが、問題を見たとき、正弦定理と余弦定理のどちらを使えばいいのか、どう考えたらいいんですか?
進研ゼミからの回答!
こんにちは。がんばって勉強に取り組んでいますね。
いただいた質問について、さっそく回答させていただきます。
【質問の確認】
【問題】
a=4, b=2, c=3である △ABCについて、次の問いに答えよ。
(1) cosA の値を求めよ。
という問題について、
解答解説1行目で「余弦定理より」とはじまっているのですが、問題を見たとき、正弦定理と余弦定理のどちらを使えばいいのか、どう考えたらいいんですか?
というご質問ですね。さっそく見ていきましょう。
【解説】
三角形の辺の長さや角の大きさを求めたいときは、正弦定理や余弦定理が有効ですが、その際、どちらを使えばよいのかは、確かに迷うところですね。
そこでまず、各々の定理について確認しておきましょう。
下の図のように3辺の長さがa, b, cで、辺に対する角がA, B, Cである△ABCで考えましょう。
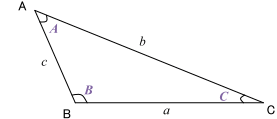

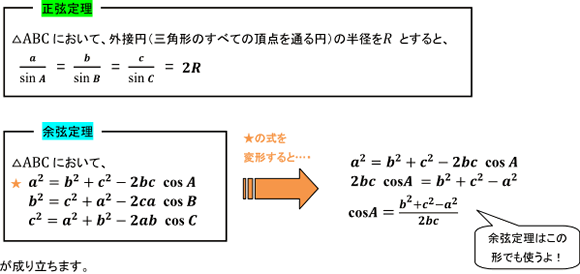

ここで、2つの定理の使い分けを見ていきましょう。
「わかっている条件」と「求めたいもの」を確認して以下の使い分けを確認してみましょう。
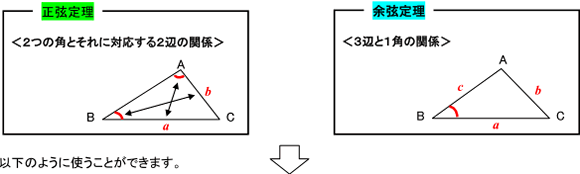

◆三角形の“1辺の長さ” と “2つの角の大きさ” が与えられた場合
⇒ 正弦定理を用いて、“残りの2辺の長さ” を求めることができる。
◆三角形の“2辺の長さ” と “1つの角の大きさ” が与えられた場合
⇒ 余弦定理を用いて、“残りの辺の長さ” を求めることができる。
◆三角形の“3辺の長さ” が与えられた場合
⇒ 余弦定理を用いて、すべての角の余弦が求められ、すべての“角の大きさ”を考えることができる。
そこで、本問を見てみましょう。
今、わかっているのは、3辺の長さ、そして求めたいのはcosAの値です。
これらがすべて登場するのは余弦定理ですね。それで、(1)では余弦定理を利用したわけです。
基本の式を![]() と変形し、a=4,b=2,c=3を代入すればよいですね。
と変形し、a=4,b=2,c=3を代入すればよいですね。
これを計算すると、 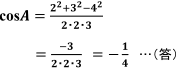
となります。
【アドバイス】
まずは、正弦定理、余弦定理を正確に頭に入れましょう。
あとは、わかっていること、求めたいもの、計算の効率などに応じてこれらを使い分ければよいですね。
基本の定理の式と同時に、今回の(1)を解く際に利用した式の形のように、
変形した式もすぐ使えるようにしておくと効率よく解くことができますよ。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「図形と計量」Q&A一覧
「図形と計量」Q&A一覧
- 【図形と計量】180°-θの三角比
- 【図形と計量】90°-θの三角比
- 【図形と計量】90°以上の角の三角比の値について
- 【図形と計量】cosの値が負になるときの角度の求め方
- 【図形と計量】sinを含む分数の式の計算方法
- 【図形と計量】sin,cos,tanの値の覚え方
- 【図形と計量】tanの値からcosの値を求めるときの分数の式変形について
- 【図形と計量】「なす角」の意味
- 【図形と計量】三角形における三角比の値
- 【図形と計量】三角形の3辺が与えられたときの面積の求め方
- 【図形と計量】三角形の辺の長さを求めるときの三角比の値
- 【図形と計量】三角比の値について
- 【図形と計量】正弦定理から,三角形の辺の長さを求める計算について
- 【図形と計量】正弦定理と余弦定理のどっちを使えばいいんですか?
- 【図形と計量】正弦定理より辺の長さを求める式変形の方法
- 【図形と計量】角度の場合分けについて












