【図形と計量】90°以上の角の三角比の値について

【質問の確認】

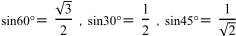　というのはわかるのですが，sin120°などそれ以外の角度になるとイコールのあとがわかりません。（sin 120°＝？）

というご質問ですね。

【解説】

1つの角が120° のような，鈍角（90° ＜θ ＜180°）の，直角三角形はつくることができませんね。
そこで，鈍角の場合も含めて，0°≦"θ" ≦180° の範囲で三角比を考えるためのルールである座標を用いた定義を利用することになります。

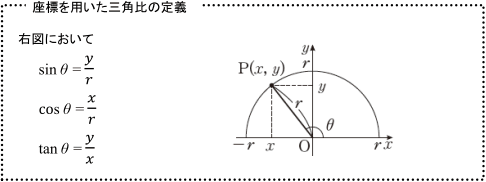
実際には，半径 r を１として考えることが多いので，次のように

となります。
この，「定義」というのは，「ことばの約束」なので，覚えて使うことです。

≪sin120°，cos120°の値≫
では，sin120°やcos120°の値を求めてみましょう。
まず，120°になる点Pをとってみると，下図のようになります。点Pのx 座標とy 座標がわかればよいわけです。そこで，図の青い三角形に着目すると，１つの内角が60°の直角三角形ですから辺の比が1：2：　であることがわかります。
だから，斜辺を1とすると，それぞれの辺の長さは，
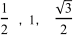　となります。
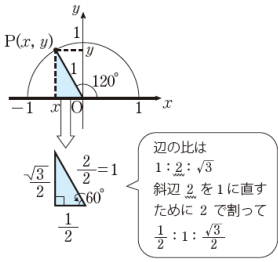
また，点Pのある場所で，そのx ，y の符号をとらえます。
ですから，下図の場合，y はプラス，x はマイナスになります。

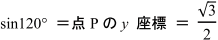
x座標は長さが　　ですが， y軸の左側にあるので，マイナスの値で，

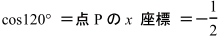
となります。
長さは，直角三角形の辺の比でとらえますが，符号は点Pの位置でとらえなくてはなりません。
これは，角度が180°を超えても，同じ考え方で，今後ずっと使っていきます。
このように，約束と，その意義を，セットで，頭に入れるところから始めなければなりませんが，そこがわかると，90°より大きい角の三角比が使えるようになります。

【アドバイス】

今後，角度はどんどんと拡張されていきますので，今のうちに，三角比が負の値になる場合の求め方を身につけておきましょう。まず，単位円をかき，角θを，x軸の正のほうからとります（これも約束です）。そして，円周上に点Pをとって，sinθはy座標の値，cosθはx 座標の値でとらえます。大事なのは，円をかいて確認して求めるということです。習慣づけると，ミスしない力になります。

では，ここまでです。ゼミの教材を学習に役立てて，力をつけていってください。応援しています。