【図形と計量】正弦定理から,三角形の辺の長さを求める計算について
正弦定理から,三角形の辺の長さを求める計算について
△ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。
という問題がありますが, これを定理にあてはめていって,
b = 3 / sin60°× sin45°
まではつくれるんですが,そこから
(3 ÷ √3/2 ) × 1/√2= 6/√6=√6
というのになるのが,意味がわかりません。 なぜルートが出てくるのですか?
(3 ÷√3/2)×1/√2が,もう何が何だかわかりません。どこから√ が現れたんですか?
どこにも二乗とかないのに。
これでもか!というぐらい細かく教えてください。
進研ゼミからの回答!
こんにちは。早速あなたの質問にお答えします。
【質問の確認】
△ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。
という問題がありますが,正弦定理にあてはめていって,
![]()
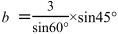
まではつくれるんですが,そこから
![]()
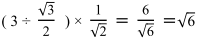
というのになるのが,意味がわかりません。なぜルートが出てくるのですか?
というご質問ですね。
【解説】
≪30°,45°,60°の三角比の確認≫
まず,30°,45°,60°の角をもつ特別な直角三角形の3辺の比を確認しておきましょう。


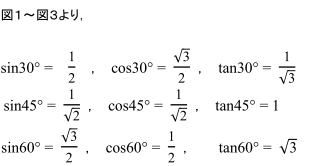
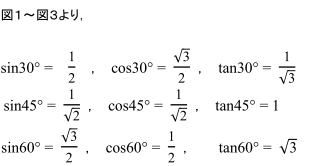
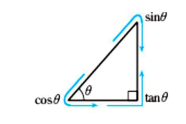

ですね。上記の30°,45°,60°の三角比は,いつでも使えるようにしておくことが大切です。
≪正弦定理を用いて三角形の辺の長さを求める≫
では,
問題
△ABCにおいて,a=3,A=60°,B=45°のとき,bを求めよ。
を解いてみましょう。
aとA,bとBは向かい合う辺と角だから,
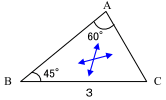

正弦定理 ![]()
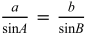 より,
より,![]()
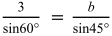
両辺にsin45°を掛けて,
![]()
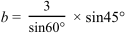
ここまで変形したら,![]()
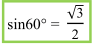 ,
,![]()
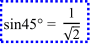 を代入します。
を代入します。
すると,
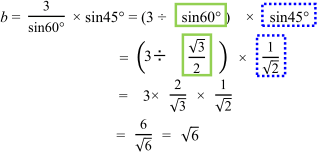
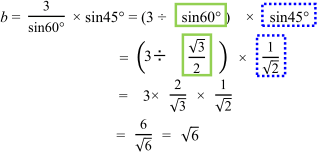
が導かれます。
【アドバイス】
正弦定理や余弦定理と同じように,
30°,45°,60°の三角比は,いつでも使えるように覚えておきましょう。
これからもゼミの教材を活用して頑張ってください。
ではまたわからないことがあったら質問を送ってくださいね。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「図形と計量」Q&A一覧
「図形と計量」Q&A一覧
- 【図形と計量】180°-θの三角比
- 【図形と計量】90°-θの三角比
- 【図形と計量】90°以上の角の三角比の値について
- 【図形と計量】cosの値が負になるときの角度の求め方
- 【図形と計量】sinを含む分数の式の計算方法
- 【図形と計量】sin,cos,tanの値の覚え方
- 【図形と計量】tanの値からcosの値を求めるときの分数の式変形について
- 【図形と計量】「なす角」の意味
- 【図形と計量】三角形における三角比の値
- 【図形と計量】三角形の3辺が与えられたときの面積の求め方
- 【図形と計量】三角形の辺の長さを求めるときの三角比の値
- 【図形と計量】三角比の値について
- 【図形と計量】正弦定理から,三角形の辺の長さを求める計算について
- 【図形と計量】正弦定理と余弦定理のどっちを使えばいいんですか?
- 【図形と計量】正弦定理より辺の長さを求める式変形の方法
- 【図形と計量】角度の場合分けについて












