【図形と計量】角度の場合分けについて
角度の場合分けについて
ここでは0°≦θ≦90°,90°<θ≦180°となっていますが,
sinθ=3/7 のときcosθ ,tanθを求めるときの場合分けは0°<θ<90,
90°<θ <180°と学校のワークに書かれています。
=のつけ方がよくわかりません。
進研ゼミからの回答!
こんにちは。いただいた質問について早速お答えします。
【質問の確認】
【問題】
0°≦θ≦180° とする。sin θ = ![]()
![]() のとき,cos θ ,tan θ の値を求めよ。
のとき,cos θ ,tan θ の値を求めよ。
【解答解説】から抜粋部分


この解答の
(ⅰ)0° ≦ θ ≦ 90° のとき
(ⅱ)90° < θ ≦ 180° のとき
の場合分け(解答中の ![]()
![]() の部分)を,学校のワークでは
の部分)を,学校のワークでは
(ⅰ)0° < θ < 90° のとき
(ⅱ)90° < θ < 180° のとき
としていて,
= のつけ方がよくわかりません。
というご質問ですね。
【解説】
ここでは,θ の範囲が0°≦θ≦180° と与えられていることから,解答では,この範囲を
![]()
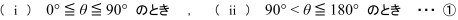
の2つに分けて考えていました。
また,条件sin θ = ![]()
![]() より,θ が0°,90°,180° となることはないので,学校のワークのように,
より,θ が0°,90°,180° となることはないので,学校のワークのように,
![]()
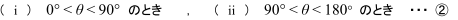
と分けることも可能です。
ただし,②の場合分けを用いる場合には,なぜ②のように場合分けをすることができるのか,理由を簡単に説明しておく方がよいでしょう。
なぜならば,②の場合分けでは,問題で与えられたθの範囲( 0°≦θ≦180°) のうち,θ = 0°,90°,180°が含まれていないからです。


というように,簡単に説明を加えておきましょう。
【アドバイス】
細かいところにまで注意をして考えられていましたね。ぜひもう一度①,②の場合分けの違いについてじっくり考えてみてください。
これからもがんばってくださいね。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「図形と計量」Q&A一覧
「図形と計量」Q&A一覧
- 【図形と計量】180°-θの三角比
- 【図形と計量】90°-θの三角比
- 【図形と計量】90°以上の角の三角比の値について
- 【図形と計量】cosの値が負になるときの角度の求め方
- 【図形と計量】sinを含む分数の式の計算方法
- 【図形と計量】sin,cos,tanの値の覚え方
- 【図形と計量】tanの値からcosの値を求めるときの分数の式変形について
- 【図形と計量】「なす角」の意味
- 【図形と計量】三角形における三角比の値
- 【図形と計量】三角形の3辺が与えられたときの面積の求め方
- 【図形と計量】三角形の辺の長さを求めるときの三角比の値
- 【図形と計量】三角比の値について
- 【図形と計量】正弦定理から,三角形の辺の長さを求める計算について
- 【図形と計量】正弦定理と余弦定理のどっちを使えばいいんですか?
- 【図形と計量】正弦定理より辺の長さを求める式変形の方法
- 【図形と計量】角度の場合分けについて












