【場合の数と確率】A∩B全体に ̄がつく集合
A∩B全体に ̄がつく集合
A∩B ̄が図のどの部分になるのかわからない。A∩B ̄ の意味がわからない。
進研ゼミからの回答!
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
![]() は,図のどの部分になるのかわからない。
は,図のどの部分になるのかわからない。![]() の意味がわからない。
の意味がわからない。
というご質問ですね
【解説】
≪ ̄の意味≫
![]() の上にある ̄は,
の上にある ̄は,![]() の ̄と同じ記号で,「補集合」を表しています。
の ̄と同じ記号で,「補集合」を表しています。
![]() と
と ![]() を比べながら,もう少し詳しく説明しましょう。
を比べながら,もう少し詳しく説明しましょう。
まず,A,Bを全体集合Uの部分集合とします。
![]() は,Aの補集合で,「Aに属さない要素全体の集合」を表しています。
は,Aの補集合で,「Aに属さない要素全体の集合」を表しています。
![]() のように,∩や∪で表された集合全体に ̄がついているときも,
のように,∩や∪で表された集合全体に ̄がついているときも,![]() と同じように考えます。
と同じように考えます。
つまり,
![]() は,A∩Bの補集合で,「A∩Bに属さない要素の集合」
は,A∩Bの補集合で,「A∩Bに属さない要素の集合」
を表しているということです。
AやA∩B などの集合を,★とすると,
![]() は「★の補集合」で,「★に属さない要素全体の集合」
は「★の補集合」で,「★に属さない要素全体の集合」
そして, ∩や∪で表された集合全体に ̄がついているときは,次の手順でその集合を把握するとよいでしょう。
∩や∪で表された集合全体に ̄がついた集合を図示する手順
①まずは,![]() の ̄の下に書いてある「★」がどんな集合かをとらえる。
の ̄の下に書いてある「★」がどんな集合かをとらえる。
②①でとらえた★に「属さない要素」を考える。
この手順に従って,![]() を図示してみましょう。
を図示してみましょう。
【問題】 ![]() を図示せよ。
を図示せよ。
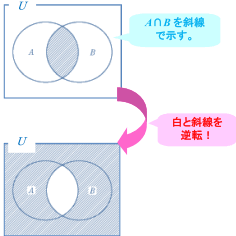
①まず,![]() の ̄の下に書いてあるA∩Bを図で表すと,下の図のようになります。
の ̄の下に書いてあるA∩Bを図で表すと,下の図のようになります。
このとき, ̄のことはまだ考えなくて大丈夫です。
②次に, ̄(補集合)のことを考えましょう。
![]() は,「A∩Bに属さない要素全体の集合」でした。
は,「A∩Bに属さない要素全体の集合」でした。
そこで,①でかいたA∩Bに属さない要素の集合を考えればよいのです。
すると,下のようになります。
つまり,①のA∩Bの図の「白」と「斜線」の部分を逆転させた部分が ![]() を表す集合となるわけです。
を表す集合となるわけです。

【アドバイス】
![]() は「★の補集合」で,「★に属さない要素全体の集合」であることをしっかりと覚えて,
は「★の補集合」で,「★に属さない要素全体の集合」であることをしっかりと覚えて,![]() の集合を図示できるようにしておきましょう。そして,集合の図を見て,その意味を考えられるようにしておくとよいでしょう。
の集合を図示できるようにしておきましょう。そして,集合の図を見て,その意味を考えられるようにしておくとよいでしょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「場合の数と確率」Q&A一覧
「場合の数と確率」Q&A一覧
- 【場合の数と確率】A∩B全体に ̄がつく集合
- 【場合の数と確率】A ̄∪Bの図
- 【場合の数と確率】∪と∩の違い
- 【場合の数と確率】「どちらか一方」と「少なくとも一方」
- 【場合の数と確率】「同様に確からしい」の意味
- 【場合の数と確率】「条件つき確率」と「確率の乗法定理」の関係
- 【場合の数と確率】余事象を使った解き方
- 【場合の数と確率】倍数の個数の求め方
- 【場合の数と確率】区別がない組分け
- 【場合の数と確率】和の法則と積の法則の使い分け
- 【場合の数と確率】和の法則と積の法則の使い分けについて
- 【場合の数と確率】和の法則と積の法則の使い分けの仕方
- 【場合の数と確率】問題文の意味の取り方について
- 【場合の数と確率】排反事象と独立試行の違い
- 【場合の数と確率】組分けの問題の見分け方
- 【場合の数と確率】順列と組合せの見分け方












