【場合の数と確率】A ̄∪Bの図
A ̄∪Bの図
A ̄∪BやA ̄∩B のように,どちらかの集合に ̄がついている場合,図がかけません。
進研ゼミからの回答!
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
![]() やのように,どちらかの集合に
やのように,どちらかの集合に![]() がついている場合,どのような図になるのか。
がついている場合,どのような図になるのか。
というご質問ですね。
【解説】
![]() の場合,その手順は,
の場合,その手順は,
(1)![]() の図を斜線でかく。
の図を斜線でかく。
(2)(1)でかいた斜線の図に,Bの図を重ねて斜線でかく。
(3)(2)の図で,「∪のときは,すべての斜線部分を足し合わせた部分」,「∩のときは,斜線が重なった部分」となる。
です。このようにすれば,![]() の集合の図がかけます。
の集合の図がかけます。
基本的に,Aでも![]() でも手順は変わりません。
でも手順は変わりません。
補集合か,そうでないかに気をつけて図をかけばよいだけです。
≪![]() (「∪」のとき)≫
(「∪」のとき)≫
手順に従って考えていきましょう。
まず,全体集合をUとします。図を考える前段階として,下のような図をかいておきます。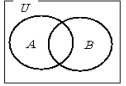

(1)まずは,![]() の中にある集合
の中にある集合 ![]() の図を斜線でかきます。
の図を斜線でかきます。![]() は,Aの補集合なので,下のような斜線の部分となります。
は,Aの補集合なので,下のような斜線の部分となります。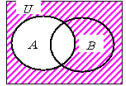

(2)次に,Bの図を重ねて斜線でかきます。
(1)と区別をつけるために,下の図のように逆方向の斜線にするとよいでしょう。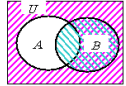

(3)(2)で2つの斜線部分を足し合わせたところが,![]() の集合を表す部分です。
の集合を表す部分です。
∪のときは,「 ![]() または B 」なので,斜線部分を「足し合わせたすべての部分」が
または B 」なので,斜線部分を「足し合わせたすべての部分」が ![]() の集合の範囲となります。
の集合の範囲となります。
よって,![]() を表すのは下の図の斜線部分になります。
を表すのは下の図の斜線部分になります。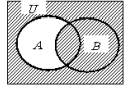

≪![]() (「∩」のとき)≫
(「∩」のとき)≫
同じ要領で図をかいて考えてみましょう。
(1)![]() の図を斜線でかきます。
の図を斜線でかきます。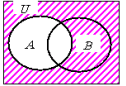

(2)次に,Bの図を重ねて斜線でかきます。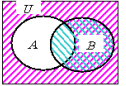

ここまでは,![]() と同じです。
と同じです。
(3)「∩」のときは,「 ![]() かつ B 」なので,図の斜線が「重なった部分」が
かつ B 」なので,図の斜線が「重なった部分」が ![]() の集合の範囲となります。
の集合の範囲となります。
よって,![]() を表すのは下の図の斜線部分になります。
を表すのは下の図の斜線部分になります。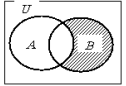

【アドバイス】
どちらかの集合に![]() がついている場合は,
がついている場合は,
★補集合を意識して図をかく。
★手間を惜しまず,1つひとつ図をかいていく。
★∪,∩をしっかりと確認する。
という3点に注意するとよいですよ。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「場合の数と確率」Q&A一覧
「場合の数と確率」Q&A一覧
- 【場合の数と確率】A∩B全体に ̄がつく集合
- 【場合の数と確率】A ̄∪Bの図
- 【場合の数と確率】∪と∩の違い
- 【場合の数と確率】「どちらか一方」と「少なくとも一方」
- 【場合の数と確率】「同様に確からしい」の意味
- 【場合の数と確率】「条件つき確率」と「確率の乗法定理」の関係
- 【場合の数と確率】余事象を使った解き方
- 【場合の数と確率】倍数の個数の求め方
- 【場合の数と確率】区別がない組分け
- 【場合の数と確率】和の法則と積の法則の使い分け
- 【場合の数と確率】和の法則と積の法則の使い分けについて
- 【場合の数と確率】和の法則と積の法則の使い分けの仕方
- 【場合の数と確率】問題文の意味の取り方について
- 【場合の数と確率】排反事象と独立試行の違い
- 【場合の数と確率】組分けの問題の見分け方
- 【場合の数と確率】順列と組合せの見分け方
- 【場合の数と確率】確率計算の公式は覚えているけど、どこで使うか分からない












