【場合の数と確率】倍数の個数の求め方

【質問の確認】

について、どうやって1〜100までの整数のうち3の倍数や5の倍数でない整数の個数を導き出すかについてですね。

【解説】

集合の要素の個数を考える問題で、3の倍数や、5の倍数でないものを、どのように導きだすのかよく分からない・・・ということですね。

まず（１）について、
ひとつ、具体例で、考えてみましょう。

≪（例）　1から10までの自然数において、3の倍数は？・・・≫

次の問題も、上の例と同じ考え方で、求めることが出来ます。

≪（１）「３の倍数である整数の個数」を求める問題≫

ここでは、「1から100までの整数」の中で、3の倍数の個数を考えるので、3×（整数）で表される、一番大きい（整数）を、求めてみましょう。

100÷3　を計算します。

100÷3= 33・・・1 (100 = 3×33+1)

商は、「33」となることから、　「33個」と分かります。

これを、集合の要素の形で表すと、解答解説のように

A={3∙1,　3∙2,　3∙3,・・・,　3∙33 }

と表せるわけです。

次に

≪（２）「５の倍数でない整数」を求める問題≫

1, 2, 3, 4, 6, 7, 8, 9, 11,・・・・などと、５の倍数ではないものを、考えると数が多くて、数えるのも大変そうです。
そこで、『「５の倍数」の個数を調べて、１００から引く』のが簡単・・・と考えることが、ポイントです。

5の倍数は、（１）の３の倍数の個数を数えたのと、同じように考えてみましょう。

として、求めることができます。

次に

≪（３）「３の倍数かつ５の倍数である整数の個数」を求める問題≫

「３の倍数かつ５の倍数」ということは、15, 30, 45, 60　・・・のような整数ですから、

と考えることが、ポイントです。　１５の倍数を（１）と同様に考えて求めてみましょう。

最後に

≪（４）「３の倍数または５の倍数」を求める問題≫

これは、具体的には、

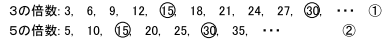
より、①、②の数を数えて、「①＋②」　をすれば良いのですが、注意点がひとつ。 ○で囲んだ整数は、①にも②にも含まれるので、２回数えていることになります。

よって、

と計算することが、ポイントです。

【アドバイス】

今回の問題を通して、「３の倍数」の個数や、「かつ」・「または」を考えるときのポイントなどをおさえておきましょう。その上で、（２）のように「〜でない」場合の数を数えるときには、「〜〜である」ものの数を数えて、全体から引く　という考え方を、身につけておくと良いですね。

今後も、分からないところは早めに解決しながら、数学に取り組んでいってくださいね。