【２次関数】２次関数のグラフとx軸の位置関係

【質問の確認】

２次関数のグラフと x軸の位置関係がわかりません。
というご質問ですね。

【解説】

２次関数のグラフは，頂点の座標により，グラフの位置が動きます。その関係を見ていきましょう。

≪x 軸と交わる様子に着目≫
「２次関数のグラフ」と「x 軸」に注目して，この２つの図形が交わる様子を表現すると…

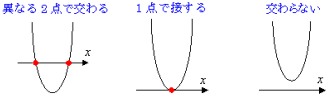
この３つのパタ−ンがあることがわかりますね。

≪共有点に着目≫
２次関数のグラフと x軸が共有する点，つまり，下の赤い点を「共有点」といいます。

この「共有点」の個数で，位置関係を表現すると，

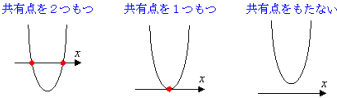
という同様の３つのパタ−ンになります。

≪実数の解の個数に着目≫
２次関数を　y ＝ a x²＋b x＋c とすると x軸は，y＝0と表現できますね。２次関数のグラフと x軸の「共有点」の座標は，y＝a x²＋b x＋c と y＝0を連立して得られる２次方程式ax²＋bx＋c＝0 の実数の解として求めることができます。（つまり，上の図の共有点 ●のx座標は，この ax²＋bx＋c＝0の実数の解です。）
例えば，y＝x²−3x＋2のグラフは次のようになります。

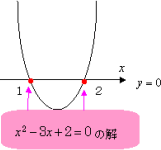
この「実数の解」の個数で，位置関係を表現すると，

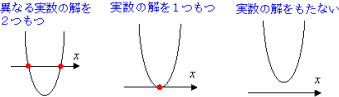
という３つのパタ−ンになります。

◎実数の解の個数の応用◎
実数の解の個数というのは，２次方程式　ax²＋bx＋c＝0 から，次の判別式で簡単に求めることができます。
２次方程式　ax²＋bx＋c＝0  は，解の公式 を用いれば，すべての解が求まりますね。そこで，これを使って実数の解の個数を調べましょう。

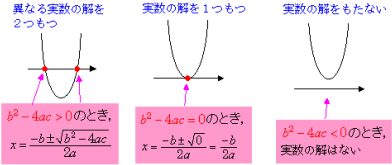
これらのグラフは，b²−4ac の符号により，３つのパタ−ンのどれかに決まることがわかりますね。
つまり，D＝b²−4ac とすると，

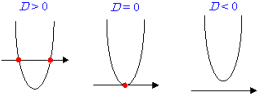
このように，２次方程式 ax²＋bx＋c＝0 から判別式 D＝b²−4acの符号を調べれば，簡単に２次関数のグラフと x軸の位置関係を知ることができます。

【アドバイス】

２次関数　y＝ax²＋bx＋c のグラフとx軸の位置関係は，y＝0とおいた２次方程式ax²＋bx＋c＝0 の判別式
D＝b²−4ac の符号から求められます。この結果だけを暗記するのでなく，上で説明したようになぜ判別式の符号から求められるかをしっかり理解しておくことが大切です。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。