【２次関数】「２次関数のグラフとx軸の共有点」と「２次方程式の解」

【質問の確認】

「２次関数のグラフとx軸の共有点」を求めるのに，「２次方程式」を解くのはなぜ？
というご質問ですね。

【解説】

≪まずは復習から　〜y軸との共有点〜≫
次のような１次関数は，中学で学びましたね。まずは，これを例に，グラフと切片の関係をつかんでいきましょう。

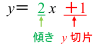
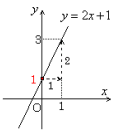
このグラフ（直線）は，２点 (0，1)，(1，3) を結んでかくことができます。

ここで，y切片，つまり，y軸との共有点の座標は１ですね。式で，y＝ ax＋bのbが，y軸との共有点の座標だと覚えていればすぐにわかりますが，ここでは，y軸との共有点の座標が１になる理由を考えてみましょう。
y軸上の点は，

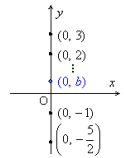
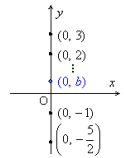
のように，すべて (0，b) の形で表すことができます。つまり，x座標は，0ですね。y切片を求めるには，x座標が0となるy＝2x＋1のグラフ上の点の座標，つまり，x＝0のときのy座標を求めればよいのです。
y＝ 2x＋1に，x＝0を代入して，
y＝2×0＋1 ＝1

よって，y切片は１になるのです。

 ≪１次関数のグラフとx軸との共有点は・・・？≫
では，x軸との共有点はどのようにして求めればよいでしょうか。
(1)の結果から予測すると，y＝2x＋1に，y＝0を代入すればよいのです。というのも，x軸上の点は,

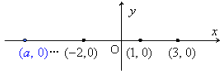
このように，すべて (a，0) の形で表すことができます。したがって，y座標が0となるグラフ上の点のx座標，つまり，y＝0のときのx座標を求めればよいのです。
y＝2x＋1に，y＝0を代入して,

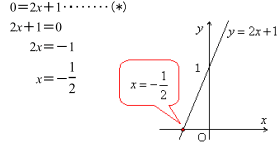
よって，この１次関数のグラフとx軸の共有点を求めるとき，(*)という式になりました。これは，１次方程式ですね。つまり， １次関数y＝ax＋bのグラフとx軸の共有点のx座標は，１次方程式ax＋b＝0の解である，といえるのです。

≪２次関数のグラフとx軸の共有点では・・・≫
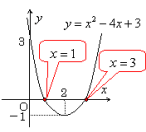これは，２次関数のときも同様です。
y＝x²−4x＋3のグラフとx軸の共有点の座標は，
（x，0）とおけるので，y＝x² − 4x ＋ 3 で，y ＝ 0として，
0＝x²−4x＋3
この2次方程式x²−4x＋3＝0を解いて，
(x−1)(x−3)＝0
よって，x ＝1，3

したがって，２次関数 y＝ax²＋bx＋c のグラフとx軸の共有点のx座標は，２次方程式ax²＋bx＋c＝0の解であるといえます。

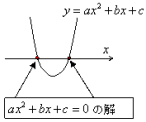
≪そして，おまけ≫
グラフが「上に凸」のときは，両辺に−１を掛けて，x²の係数を正の数にした方が計算しやすくなりますよ。

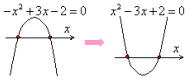
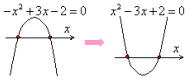
【アドバイス】

２次関数 y＝ax²＋bx＋c のグラフとx軸の共有点の座標は，（x，0）とおける，すなわち，y＝0であることを理解しておきましょう。そうすると，２次関数 y＝ax²＋bx＋c のグラフとx軸の共有点のx座標は，２次方程式ax²＋bx＋c＝0の解であることがわかりますね。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。