【式と証明】不等式の証明で相加平均と相乗平均の大小関係を使うコツ

【質問の確認】

不等式の証明で，どんなときに，相加平均・相乗平均の関係を使ったらよいのかわかりません。
というご質問ですね。

【解説】

相加平均と相乗平均の大小関係は，

「a>0，b>0 のとき，（等号が成り立つのは，a=bのとき）」

でしたね。
この関係は，不等式を証明するときなどに使うことができるものでした。
ただし，実際の問題では，どんなときに相加平均と相乗平均の大小関係を使ったらよいのか，どのような２数に対して当てはめればよいのか，迷うことがあると思います。
では，具体的に見ていきましょう。

≪その1：どんなときに，相加平均と相乗平均の大小関係を使ったらよいの? ≫
判断するポイントは，次の通りです。

①　証明する不等式の中に，a， のように，「掛けたら文字が消えてしまう（定数となる）文字のカタマリの組」があること。
（a× = 1となり，a が消えます）。

②　①の文字のカタマリのそれぞれが，正の数（値）であること。
（例えば，a， がともに正の数）。

次の例題で，どのように使うかを考えてみましょう。

＜考え方＞
式の中で，「カタマリ」を設定します。例えば，ab， という2つのカタマリとして見てみると，

◆ab， を掛けると，ab × = 9となり，abが消えて定数となる。
よって，上のポイント①に当てはまります。

◆a > 0，b > 0だから，ab > 0， > 0
よって，上のポイント②に当てはまります。
このように，上記２つのポイントを満たしているので，ab， に対して，相加平均と相乗平均の大小関係が使えそう，と判断できますね。

＜解答＞

このように，どの2つをカタマリと設定するかが肝心ですが，これは，先のポイント①②を意識して問題を解くことで慣れていきましょう。

≪その2：相加平均と相乗平均の大小関係を使える気がするけれど，そのやり方がわからない…という場合≫
難しい問題になると，なんとなく相加平均と相乗平均の大小関係が使えそうなのですが，どの２式を当てはめたらよいのかわかりにくいことがあります。その場合の考え方について見てみましょう。

（考え方）
式の中に，2a， やb， があるので，先のポイント①②は満たしているように感じます。しかし，どの２式に対して相加平均と相乗平均の大小関係を当てはめたらよいのか迷ってしまいますね。
上記のポイント２点は満たしていそうだけれど，どの文字のカタマリに注目してよいかわかりにくいときは，証明すべき不等式の左辺を展開して，どの文字のカタマリがポイント①②を満たすか考えましょう。

不等式の左辺を展開し，整理することで， というカタマリが見えてきました。
× = 1より，ポイント①が成り立ちます。また，a ＞ 0，b ＞ 0より　 > 0， > 0　ですから，ポイント②が成り立ちます。だから，， に対して，相加平均と相乗平均の大小関係を使えることがわかります。

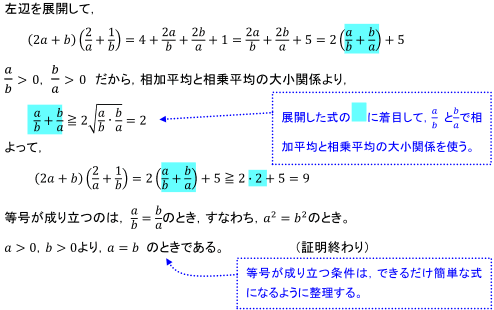
＜解答＞

---

◎まとめ
不等式の証明で，相加平均と相乗平均の大小関係を使うかどうか，判断のポイントは，

①　証明する不等式の中に，「掛けたら定数となるような文字のカタマリの組」があること。

②　①の文字のカタマリのそれぞれが，正の数（値）であること。

そして，「①②に当てはまるかどうかすぐにわからない」というときは，「証明すべき不等式を展開」して，上の①②を満たす文字のカタマリがあるかチェックしましょう。

【アドバイス】

『相加平均と相乗平均の大小関係』を使うと楽に証明できる場合もあるので，判断のポイントをしっかり押さえて，使えるようになっておきましょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。