【図形の性質】平行線の作図(内分点,外分点の作図について)
平行線の作図(内分点,外分点の作図について)
内分点,外分点の作図のときに,平行線の作図をしないといけないみたいなんですけど,平行線の作図がよくわかりません。詳しく回答してくれると助かります。
進研ゼミからの回答!
こんにちは。
いただいた質問について,さっそく回答させていただきます。
【質問の確認】
内分点,外分点の作図のときに,必要になる平行線の作図がよくわかりません。
というご質問ですね。
【解説】
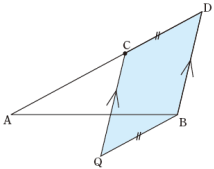
線分ABを3:2の比に内分する点を作図するときを説明しましょう。まず,AC:CD=3:2 となる点C,Dを作図するところまではいいですね。次に,点Cを通り線分BDに平行な直線を作図してみます。
このとき,平行四辺形BDCQを作図することを考えるとわかりやすいですよ。つまり,CD=QB,BD=QCとなるような点Qを作図すればいいのです。

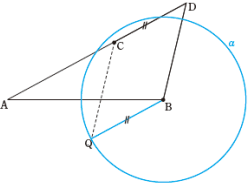
①CD=QBとなる点Qを求めるために,点Bを中心とし線分CDの長さを半径とする円αをかきます。

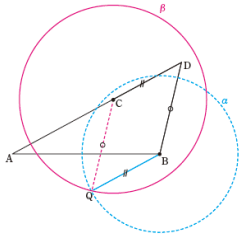
②BD=QCとなる点Qを求めるために,点Cを中心とし線分BDの長さを半径とする円βをかきます。

③2円α,βの2つの交点のうち,直線BDに関して点C側にある点Qと点Cを結ぶと,平行四辺形BDCQを作図することができます。
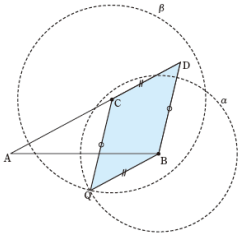

よって,BD//QCとなり,ABとCQの交点が,線分ABを3:2の比に内分する点となります。
線分ABを3:2の比に外分する点も同様に平行線を作図して求めてくださいね。
【アドバイス】
平行四辺形を作図することによって平行な直線を得ることができますが,おわかりいただけましたか?
それではこれで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「図形の性質」Q&A一覧
「図形の性質」Q&A一覧
- 【図形の性質】チェバの定理(三角形の頂点を通る3つの直線が三角形の外部で交わるとき)
- 【図形の性質】内分点と平行線の作図の仕方について
- 【図形の性質】図形の証明の考え方
- 【図形の性質】外分点の作図の仕方
- 【図形の性質】平行線の作図(内分点,外分点の作図について)
- 【図形の性質】方べきの定理ってどういうときに出てくるんですか?
- 【図形の性質】メネラウスの定理とは?証明・覚え方・チェバの定理との違いも知りたい












