【図形の性質】チェバの定理(三角形の頂点を通る3つの直線が三角形の外部で交わるとき)
チェバの定理(三角形の頂点を通る3つの直線が三角形の外部で交わるとき)
点Oが三角形ABCの外にあって,直線AO,BO,COとそれぞれの対辺の延長が交わるとき,どのようにチェバの定理を使えばいいのかわかりません。どこから始まってどこで終わるのかなどを教えてください。
進研ゼミからの回答!
数学の勉強にがんばって取り組んでいますね。質問をいただいたのでお答えします。
【質問の確認】
点Oが三角形ABCの外にあって,直線AO,BO,COとそれぞれの対辺の延長が交わるとき,どのようにチェバの定理を使えばいいのかわかりません。どこから始まってどこで終わるのかなどを教えてください。
というご質問ですね。
【解説】
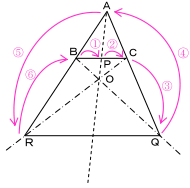

チェバの定理で点Oが△ABCの外にあるときというのは図のような場合ですが,このときも,
P:直線AOと直線BCの交点
Q:直線BOと直線ACの交点
R:直線COと直線ABの交点
とすれば,点Oが内部にあるときと同じ
![]()
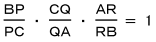
という関係式が成り立ちます。
点P, Q ,R の位置をしっかりとつかめば,点Oが△ABCの内部か外部かに関係なく
![]()
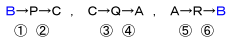
という順番,すなわち,頂点→分点→頂点→分点→ ・・・・・・
と頂点と分点を交互にたどっていって,もとの点に戻ればよいのです。
これは,点Oが三角形の内部にあるときと同じです。
どこからはじめても,最後ははじめの点に戻ります。
【アドバイス】
点Oが△ABCの外部にあるときも,
直線AO上の点がP ,直線BO上の点がQ ,直線CO上の点がRとなることを押さえておけば,点Oが内部にあるときの公式と同じです。
点P,Q,R の位置をしっかりつかんで,内部でも外部でも同じ関係式が成り立っていることをよく理解しておきましょう。
では,この調子でがんばってゼミの教材に取り組み,実戦力を養っていってくださいね。
応援しています!
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「図形の性質」Q&A一覧
「図形の性質」Q&A一覧
- 【図形の性質】チェバの定理(三角形の頂点を通る3つの直線が三角形の外部で交わるとき)
- 【図形の性質】内分点と平行線の作図の仕方について
- 【図形の性質】図形の証明の考え方
- 【図形の性質】外分点の作図の仕方
- 【図形の性質】平行線の作図(内分点,外分点の作図について)
- 【図形の性質】方べきの定理ってどういうときに出てくるんですか?












