ベネッセ
会員のかた

進研ゼミ 高校講座

【図形の性質】内分点と平行線の作図の仕方について

内分点と平行線の作図の仕方について

作図で，直線l上にＡＣ：ＣＤ＝３：２となる点Ｃ，Ｄをとるとき，どうやってとりますか？？
あと，点Ｃを通り線分ＤＢに平行な直線の引き方はどうやりますか？？

進研ゼミからの回答！

こんにちは。
いただいた質問について，早速お答えします。

【質問の確認】

作図で，直線l上にＡＣ：ＣＤ＝３：２となる点Ｃ，Ｄをとるとき，どうやってとりますか？？
点Ｃを通り線分ＤＢに平行な直線の引き方はどうやりますか？？

というご質問ですね。

【解説】

≪内分点の作図≫
直線l上にＡＣ：ＣＤ＝３：２となる点Ｃ，Ｄをとる手順は次のようになります。

①点Ａを中心とする適当な半径の円と，直線lの交点をＡ1とします。

②点Ａ1を中心とする同じ半径の円と，直線l の交点をＡ2とします。

③点Ａ2を中心とする同じ半径の円と，直線l の交点をＡ3とします。

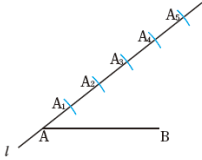同様の手順で，点Ａ4，Ａ5を，直線l 上にとります（図）。

すると，ＡＡ3 ：Ａ3Ａ5 ＝３：２ となりますので，

点Ａ3をＣ，点Ａ5 をＤ

とすれば，直線l上に ＡＣ：ＣＤ＝３：２ となる点Ｃ，Ｄがとれます。

≪平行線の作図≫
また点Ｃを通り，線分ＤＢに平行な直線を引く手順は次のようになります。

①点Ｄを中心とし，線分ＢＣの長さを半径とする円をかきます。

②点Ｃを中心とし，線分ＢＤの長さを半径とする円をかきます。

③この２円の２つの交点のうち，直線ＤＢに関して点Ｃ側にある

点をＥとして直線ＣＥを引くと，これが点Ｃを通り，線分ＤＢに平行な直線になります。

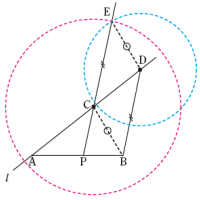
直線ＣＥが求める直線である理由は，作図の手順から，図において

ＢＣ＝ＤＥ，ＢＤ＝ＣＥ

が成り立つので，四角形ＣＢＤEが平行四辺形になっているからです。
そして，この直線ＣＥと線分ＡＢの交点をＰとおくと，点Ｐが線分ＡＢを３：２の比に内分する点になります。

【アドバイス】

このように，平行線の作図では，平行四辺形をつくり出すことで求められます。手順をしっかり覚えておきましょう。

では，これからも『進研ゼミ高校講座』を活用して，数学の力を伸ばしていきましょう。

【その他にも苦手なところはありませんか？】

わからないところをウヤムヤにせず、その場で徹底的につぶすことが苦手を作らないコツ。
「進研ゼミ」には、苦手をつくらない工夫があります。

  • 丁寧な解答解説 途中式は省略なし！詳しい内容だからわかる！
  • 万が一わからなかった場合も個別指導でニガテ解決できる！

＜進研ゼミでできること＞授業やテスト前の「わからない」を解消・苦手をつくらない

教科書別に要点をおさえて
予習復習も効率的に！

予習復習 効率UPアプリ
予習復習 効率UPアプリ
予習復習 効率UPアプリ
予習復習 効率UPアプリ

個人のニガテをAIが分析。
力が伸びる問題を自動出題。

AI StLike -個別弱点攻略AI
AI StLike -個別弱点攻略AI

詳しい講座の紹介はこちらから

まずは、学年をお選びください。

高校1年生 高校2年生 高校3年生
  • 入会金0円 入会のお申し込み
  • 無料体験教材・資料のお申し込み
  • お友だち・ごきょうだい紹介制度
受講費・受講システムを確認

2018年度入試 合格速報

進研ゼミで大学合格！
今年も喜びの声ぞくぞく！

読み込みに失敗しました。
進研ゼミ高校講座について詳しく見る

進研ゼミ『高校講座』関連商品・サービス

一番上に戻る

進研ゼミ 高校講座
会員向けページにようこそ

会員のかた
進研ゼミ 高校講座 ご受講のかた
保護者のかた
進研ゼミ 保護者通信

高校講座 オプションお申し込み(有料)

各種お手続き

受験プラン・コース変更、教科・科目の追加 登録内容(住所・電話番号・支払い方法など)の変更

受講に関するご質問ご相談など、お気軽にお問い合わせください。

お電話でのお問い合わせ

0120-507-779

受付時間：9:00～21:00（年末年始除く）

通話料無料*音声ガイダンスでご案内いたします

ご提供いただく個人情報は、お申し込みいただいた商品・サービス提供の他、学習・語学、子育て・暮らし支援、趣味等の商品・サービスおよびその決済方法等に関するご案内、調査、統計・マーケティング資料作成および、研究・企画開発に利用します。
お客様の意思によりご提供いただけない部分がある場合、手続き・サービス等に支障が生じることがあります。また、商品発送等で個人情報の取り扱いを業務委託しますが、厳重に委託先を管理・指導します。個人情報に関するお問い合わせは、個人情報お問い合わせ窓口（0120-924721通話料無料、年末年始を除く、9時～21時）にて承ります。

（株）ベネッセコーポレーション CPO（個人情報保護最高責任者）

受講に関するご質問ご相談など、お気軽にお問い合わせください。

お電話でのお問い合わせ

0120-507-779

受付時間：9:00～21:00（年末年始除く）

通話料無料*音声ガイダンスでご案内いたします

ご提供いただく個人情報は、お申し込みいただいた商品・サービス提供の他、学習・語学、子育て・暮らし支援、趣味等の商品・サービスおよびその決済方法等に関するご案内、調査、統計・マーケティング資料作成および、研究・企画開発に利用します。
お客様の意思によりご提供いただけない部分がある場合、手続き・サービス等に支障が生じることがあります。また、商品発送等で個人情報の取り扱いを業務委託しますが、厳重に委託先を管理・指導します。個人情報に関するお問い合わせは、個人情報お問い合わせ窓口（0120-924721通話料無料、年末年始を除く、9時～21時）にて承ります。

（株）ベネッセコーポレーション CPO（個人情報保護最高責任者）

※進研ゼミ『高校講座』について。矢野経済研究所「2014年版 教育産業白書」をもとに事業者を選定し、自社による第三者機関でのインターネット調査で高校生3,000人を対象に行った2015年4月時点で利用している学習法についての調査結果より。

学年をお選びください。

高校1年生 高校2年生 高校3年生
進研ゼミ ハイブリッドスタイル 利用環境条件

「進研ゼミ　ハイブリッドスタイル」はお手持ちのiPadでご利用いただけます。

対応機種
iPad（第4世代）、iPad Air、iPad Air 2、iPad mini 2、iPad mini 3、iPad mini 4
  • OS : iOS8.3以上。
  • 容量 : 8GB程度を想定。
  • 2016年2月時点。
  • 以下の端末ではお使いいただけません。
    パソコン、スマートフォン、iPad以外のタブレット、進研ゼミでお届けしている専用タブレット
    （チャレンジパッド、チャレンジタブレット、チャレンジタブレットネクスト）
通信環境

常時接続可能なブロードバンド（光ファイバなど）環境と、無線LAN（Wi-Fi）環境をご用意ください（10Mbps以上を推奨）。
  • 上記に合致しない環境では、サービスをご利用いただけない場合があります。
  • インターネットサービスプロバイダとの契約、無線LANルータが必要となります。接続料金等はお客さまのご負担となります。
  • セルラーモデルのiPadをご利用の方も、無線LAN(Wi-Fi)環境が必要です。ただし、テザリング機能での通信は推奨いたしません。
  • Apple、Apple ロゴ、iPadは米国および他の国々で登録された Apple Inc. の商標です。
  • iPadの機種、価格、内容等は変わることがあります。
  • ＜ハイブリッドスタイル＞で使用するiPadは、「進研ゼミ」以外のアプリにも接続できるタブレットです。インターネット接続・アプリ利用等の制限については、保護者の管理・判断のもとご利用ください。

あとから紹介制度のやり方

入会後に、ご紹介者の情報を登録することもできます。入会フォームの「入会後に、ご紹介者の情報を登録する」にチェックを入れてください。

Webでお申し込みをする場合

「入会申し込みページ」の「支払方法等の選択」内にある「ご紹介者」の欄で、 「入会後に、ご紹介者の情報を登録する」を選び、そのまま次の画面に進んでください。

  • Web画面のデザインはイメージです。変更する場合があります。

お申し込みの際にご登録いただいたメールアドレスに、手続き完了のメールをお送りしますので、プレゼント申し込み手続きを行う代表者を決め、お手続きをお願いします。

  • どちらかお一人がお手続きするだけでＯＫです。

電話でお申し込みをする場合

ご入会のお申し込みをいただく際、オペレーターが「ご紹介者はいらっしゃいますか」とおうかがいします。
⇒おそれいりますが「後から申し込みます」とお答えください。

入会完了

あなたと、あなたのお友だち・ごきょうだいに「教材」をお送りしますので、
プレゼント申し込み手続きを行う代表者を決め、0120-332211（9:00～21:00年末年始除く　通話料無料）までお電話ください。 ※一部のIP電話からは042-679-8567（ただし通話料がかかります）
その際、「お友だち・ごきょうだいの紹介であること」と「ご紹介者の会員番号」を忘れずにお伝えください。どちらかお一人がお手続きをすれば、お二人分のプレゼントをお届けします。

  • どちらかお一人がお手続きするだけでOKです。

「入会申し込みページ」の「支払い方法等の選択」内にある
「ご紹介者」の欄に、紹介してくれる方の情報をご入力ください。

紹介制度フォームサンプル

【お申し込み前に必ずお読みください】

●1月号（12/27まで）にご入会した方がキャンペーン対象です。
●受講費は1ヵ月分かかります。2月号以降を継続されない場合は、支払い期間にかかわらず「毎月払い」1ヵ月分の受講費のお支払いとなります。
●1ヵ月で退会する場合は1/10までに電話連絡が必要になります。ご連絡はお電話に限ります。
●退会連絡をいただかない場合、引き続き2月号以降をお届けします。

2019年12月17日に2021年度「大学入学共通テスト」にて予定されていた国語・数学の記述式問題の導入見送りの発表が文部科学省よりございました。現在「進研ゼミ高校講座」よりお届けしているご案内について、12月17日以前の入試情報でお届けしているものがございます。
今後お届けするご案内・教材については、最新の入試情報を踏まえてお届けできるように努めてまいりますので、ご理解のほど何卒よろしくお願い申し上げます。
なお、ベネッセコーポレーションでは、新大学入試の最新情報をわかりやすく解説する「教育セミナー」（参加費無料）を全国で開催しております。これから新入試に向けて頑張る高校生のみなさま・保護者の方に、ぜひ、ご活用いただけますと幸いです。
詳しくはこちらをご覧ください。