【図形の性質】図形の証明の考え方

【質問の確認】

中学生の頃から図形の証明がとても苦手でどうやって導いていくのかがわかりません･･･
証明の仕方を覚えてしまった方がいいのでしょうか？

というご質問ですね。

【解説】

≪図形の証明のコツ≫
証明の仕方を覚えるとしても，それを応用できなければ，実際に問題を解くことに結びつきません。
なので，

・似た問題を見つけて，証明の解答の書き方をまねする

　→よく出てくる証明のパターンをつかむ

・問題の大まかな解法を覚える

　→似たような問題にあたったとき，どのような解き方をしたのか思い出せるようにする

といったことは有用なのですが，丸々証明そのものを覚えても基本的に役立ちません。

証明を苦手としている人は，うまく考え進められていないことが多いと思います。例えば，

・スタート（問題文で与えられている条件）→ゴール（証明すること）と進むことばかり考えている

・どこに目をつけたらよいか思いつかない

といったことにあてはまっていませんか。

証明問題に限らず，数学の問題を解くときには，
『最終的な結論に一気に進むことを考えるのではなく，何がわかれば結論にたどり着けそうなのかを考え，小目標を決めて，まずはその小目標を達成することを考える。』
ということが大切です。

そして，このときの小目標は，
『最終的な結論から逆にたどっていって，小目標を決める』
とよいことが結構多くあります。

≪具体的な問題で考えると・・・≫
では，ここからは具体的な問題で考えてみましょう。

図形問題なので，まずは，問題文を図に示します。△ABCと内心I ，a ，b を図にすると，
（内心が出てきたら，内接円もかきましょう。）

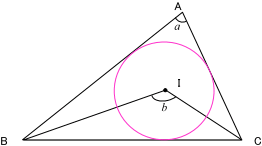
このようになります。

次に，『内心』からわかることを図にしてみましょう。ここでは「角」について証明するので， 『内心，内接円についても角の性質』 を考えると，

を使います。
「内心」「角」というキーワードから，この性質をすぐに思い出せるようにしておくことが大切です。
このことを図にすると，

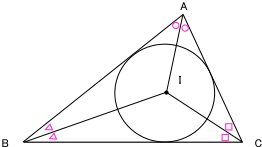
このようになります。ここまでが問題文に与えられた条件です。
　
次に，ここで証明したいことは「b＝ 90°＋ 」が成り立つことになるので，これより
『最終的な結論から逆にたどっていって，小目標を決める』
ことを考えます。

いきなりaとbの関係式を考えるのではなく，まずは「a」や「b」について，それぞれ別々に角について考えてみましょう。それには，

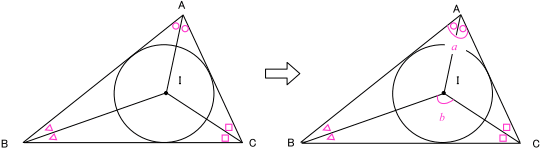
このように「a」「b」をかき込んで，関係する角の条件を探しましょう。つまり，
a，bと，○，△，□の関係式　（○，△，□は図の中に示した角）
 を考えます。これが今回の証明の『小目標』になります。

すると，
＜aについて＞
a ＝ ○ ＋ ○ ＝ 2○ ・・・（ア）
  
＜bについて＞
△IBCは，３つの角がわかっている（文字や記号がかかれている）
→三角形の内角の和は180°なので，
b ＋ △ ＋ □ ＝ 180°　・・・（イ）
が成り立ちます。

ここで，証明したい式が「b ＝ 90°＋ 」つまり，「a，b の関係式」なので，さらに，
『（ア）と（イ）を結びつける関係（○，△，□の関係）がわかれば，
「a，b の関係式」がわかりそう』
です。

そこで，○，△，□の関係も考えましょう。
△ABCの３つの内角はそれぞれ　2○，2△，2□なので，三角形の内角の和は180°より，
2○ ＋ 2△ ＋ 2□ ＝ 180°つまり，○ ＋ △ ＋ □ ＝ 90°・・・（ウ）
が成り立ちます。

ここまででわかったことは，　
a ＝ 2○           　　  ・・・（ア）
b ＋ △ ＋ □ ＝ 180°　・・・（イ）
○ + △ + □ ＝ 90°　　・・・（ウ）
です。
これをもとにa，b の関係 (b ＝ (aの式))　を導きましょう。

（イ）より，
b = 180°− (　△ ＋ □ )
 なので，（ウ）より，△ ＋ □ ＝ 90° − ○ を使えば，
b ＝ 180°− ( 90°− ○ )
＝ 90°＋ ○    ・・・（エ）
となります。

また，（ア）より，○ ＝ なので，（エ）に代入すれば，
b ＝ 90°＋
 となって証明したい式になりました。

これで証明の完成です。あとは，○，△，□といった記号を使わず，∠BAIなどを使って表して解答に仕上 げます。

また，ここで使った
・内心は，三角形の３つの内角の二等分線の交点
・三角形の内角の和は１８０°
などの基本事項もすぐに思い出せるようにしておくことが大切です。

【アドバイス】

今回説明したように，まずは下調べをして，それをまとめて解答に仕上げましょう。最初から教材などに掲載されているような解答を書く必要はありません。
こういった考え方で考えをまとめる練習を積んで，だんだんと証明問題に慣れていくとよいでしょう。

これからも『進研ゼミ高校講座』を使って，数学の力を伸ばしていってくださいね。