【積分法】面積の計算について
面積の計算について
∫f(x)dx（f(x)のaからbまでの定積分）で面積を求めようとしたら，マイナスがついてしまいました。面積なのに負になることがあるのですか？
進研ゼミからの回答！
こんにちは。
いただいた質問について，さっそく回答いたします。
【質問の確認】
で面積を求めようとしたら，マイナスがついてしまいました。面積なのに負になることがあるのですか？ というご質問ですね。
【解説】
図のような曲線 y = f (x) と x 軸，および ２直線 x = a ，x = b で囲まれた図形の面積 S は定積分を利用して，
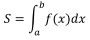
で求められます。ここはわかっているようですね。
この
を計算すると，負になってしまったのですね。
面積ですから負になるのはおかしいです。計算間違いをしていることも考えられますが，公式を利用するときに間違えている可能性が高いです。具体例を参考にしてみてください。
【例題】
放物線 y=x2-3x と x 軸で囲まれた図形の面積 S を求めよ。
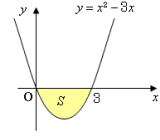まず，面積を求める図形を確認します。
図の色のついた部分が面積を求める図形ですね。
そこで，定積分より面積Sを計算すると，![S=∫0^3(x^2-3x)dx=[1/3 x^3-3/2 x^2 ]_0^3=1/3･3^3-3/2 ･3^2=9-27/2=-9/2](images/A14M1404/pic04-02.gif)
のように値が負になってしまいました。この原因は，積分区間において，f (x)≦0であるのに，そのまま積分してしまったことです。
【誤りは】区間 0 ≦ x ≦ 3 において，x2 - 3x ≦ 0 であるのに，そのまま積分してしまったこと
【正しくは】区間 a ≦ x ≦ b において，常に f(x) ≦ 0 のときは，
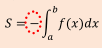
となることを利用する。
ところで，区間 a ≦ x ≦ bで常に 
のとき，曲線 y = f (x) と
，および ２直線 x = a， x = b で囲まれた図形の面積 S は，
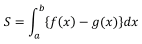
で求められることは大丈夫でしょうか？
上の【例題】でx軸を直線 y = 0 ととらえれば，２曲線 
と 
で囲まれた図形の面積を求めると考えることができます。
つまり，区間 0 ≦ x ≦ 3 で常に 
となるから，
![S=∫_0^3{0-(x^2-3x)}dx=-∫_0^3(x^2-3x)dx=-[1/3 x^3-3/2 x^2 ]_0^3=9/2](images/A14M1404/pic06-05.gif){kind=small}
と求められます。
【補足】
図のような曲線 y = f(x) と x 軸，および２直線 x = a，x = b で囲まれた図形の面積を求める場合は， x 軸との上下関係を考えて，S1 と S2 の部分に分け，場合分けをして計算する必要がありますね。
◎まとめ
面積は正でなければならない ので，負になってしまった場合は，
★ ２曲線の上下関係
★ 積分計算
に注意して，確認してみましょう。
【アドバイス】
積分を利用して面積を求めるときは，どの曲線とどの曲線に囲まれているか，そして，曲線の上下関係を押さえることがポイントです。特に，x軸と曲線で囲まれる図形の面積は上下関係を忘れやすいので，x軸を直線y=0と考えるとよいでしょう。ポイントを押さえて計算ミスをしないようにしましょう。
それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
数学のQ&Aランキング
全体のQ&Aランキング
「積分法」Q&A一覧
他の教科のQ&Aを見る【その他にも苦手なところはありませんか？】
わからないところをウヤムヤにせず、その場で徹底的につぶすことが苦手を作らないコツ。
「進研ゼミ」には、苦手をつくらない工夫があります。
＜進研ゼミでできること＞授業やテスト前の「わからない」を解消・苦手をつくらない
教科書別に要点をおさえて
予習復習も効率的に！
個人のニガテをAIが分析。
力が伸びる問題を自動出題。
