【積分法】絶対値記号を含む定積分

【質問の確認】

において，

解答のの形にもっていく方法がわかりません。
というご質問ですね。

【解説】

積分する関数に絶対値記号がついていますので，まず，積分する区間で，これをはずします。
視覚的にわかりやすくするために，グラフをかいて考えていきましょう。

≪　y＝|x²−3x＋2| のグラフをかく　≫
y＝|x²−3x＋2|…① のグラフは，y＝x²−3x＋2…② のグラフのy≦0 の部分をx軸に関して対称に折り返したものであることはいいでしょうか？

まず，②のグラフは，
y＝x²−3x＋2＝(x−1)(x−2)

と変形ができることから，x軸との共有点のx座標が1と2であるので，下図のようになります。

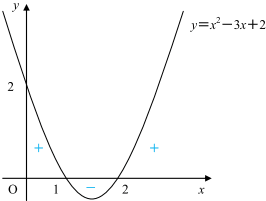
これより，　　
x≦1のとき， y≧0
1≦x≦2のとき， y≦0
2≦xのとき， y≧0
であることが読みとれます。

よって，1≦x≦2のときのy≦0の部分をx軸に関して対称に折り返すと，次のようになり，①のグラフは，青線の曲線となります。

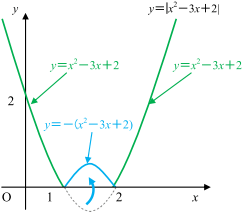
そうすると，それぞれの範囲におけるグラフの方程式は，

となります。

≪　積分区間を分割して定積分の式をつくる　≫
dxより積分区間は1≦x≦3の範囲ですが，区間1≦x≦2と区間2≦x≦3では積分する関数が異なるので，2つの区間に分けて計算します。
つまり，下の図〔ア〕の区間では，−(x²−3x＋2)を積分し，〔イ〕の区間ではx²−3x＋2 を積分します。

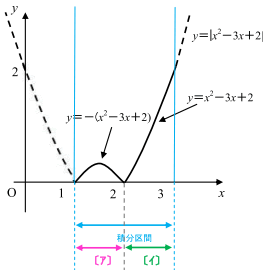
よって，〔ア〕と〔イ〕をまとめると，

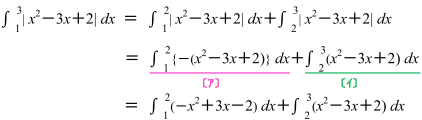
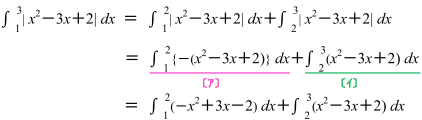
となります。

【アドバイス】

絶対値記号を含む定積分を計算するには，積分する関数のグラフをかいて，“どの区間でどの関数を積分すればいいか”を読みとって場合分けします。場合分けの仕方は理解できましたか？
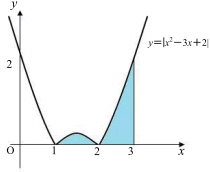
また，|x²−3x＋2|≧0となることより，与えられた定積分は，区間1≦x≦3でy＝|x²−3x＋2|のグラフとx軸で囲まれた図形の面積を表していることも確認しておきましょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。