【微分法】導関数と微分

【質問の確認】

「微分するとは，導関数を求めること」と習いましたが， とすることではないのですか？導関数 の式との関係はなんですか？
というご質問ですね。

【解説】

では「平均変化率」「微分係数」「導関数」「微分する」の関係について説明しましょう。

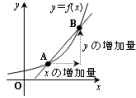
≪平均変化率とは≫
x が a から b まで変化するときの関数 y = f(x) の平均変化率は ，つまり， で求められます。

図形的には，平均変化率は２点A( a，f(a) )，B( b，f(b)) を通る直線の傾き を表しています。

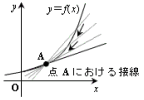
≪微分係数とは≫
この平均変化率において，b を限りなく a に近づけた値

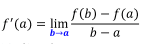
が微分係数です。

図形的には，２点A( a，f(a))，B(b，f(b)) を通る直線は，点Bを点Aに限りなく近づけるとき，点A( a，f(a)) における接線に近づくので，結果的に，微分係数は関数 y = f(x) のグラフ上の点A( a，f(a)) における接線の傾きを表しています。
ここで，「b を限りなくaに近づける」とは，「b-a=h とおくと，h→0 」であるから，
微分係数　 の式は，

と書くことができます。

≪導関数とは≫
この微分係数は，x=aをどこにとるかによって値が決まるaの関数と言えますね。この関数が導関数です。変数をxに書き換え，

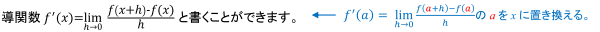
つまり， 導関数とは微分係数が求められる関数です。

≪微分するとは≫
そして，この 「導関数を求めること」を「微分する」 と言います。
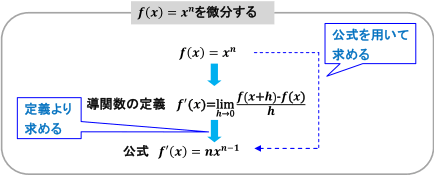
f(x)=xⁿのときは，導関数の定義より，f^'(x)=nxⁿ-1 が導かれるので，これを f(x)=xⁿ の導関数の公式として用います。

公式を使っても，定義からでも，微分することができますが，いちいち定義から求めなくてすむように公式を導いたのですから，「定義に従って求めよ。」と指示がない限り，公式を用いるとよいでしょう。

【アドバイス】

用語の意味をしっかり押さえておくことも大切ですね。
また，微分するときに，問題によって「定義に従って」とある場合もあるので，定義からでも公式からでも求められるようにしておきましょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。