【三角関数】複雑な三角関数のグラフ

【質問の確認】

のようなグラフがかけません。
というご質問ですね。

【解説】

のグラフは，y＝sinθのグラフとの関係から考えていくとよいでしょう。
さっそくグラフをかいてみましょう。

≪Step1　基本となる y = sinθ のグラフをかく≫
まず，シンプルなy = sinθ のグラフをかきます。これがおおもとになります。

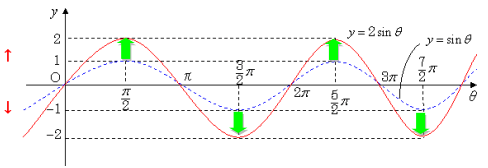
≪Step2　y = ●sinθ のグラフをかく≫
y = ●sinθ のグラフは，y = sinθ のグラフをy軸方向に●倍したグラフです。

　→ y = 2 sinθ のグラフは，Step1の y = sinθ のグラフをy軸方向に2倍します。

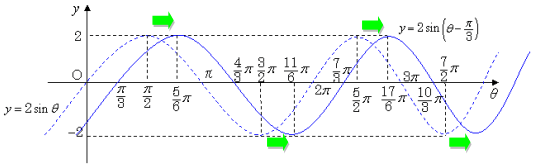
≪Step3　y = ●sin(θ - ▲) のグラフをかく≫
y = ●sin(θ - ▲) のグラフは，Step2の y = ●sinθ のグラフをθ軸方向に▲だけ平行移動します。

　→ y = 2 sin(θ - ) のグラフは，Step2でかいたグラフをθ軸方向に だけ平行移動します。

上のような手順が基本となりますので理解しておきましょう。

ここで，y ＝ asinb（θ - α）のグラフについて確認しておきましょう。

さらに， y=sinθ+■のグラフ，すなわち，y-■＝sinθのグラフは，y=sinθのグラフをy軸方向に■だけ平行移動したものであることも覚えておくといいですね。
なお，y=cosθ，y=tanθの三角関数のグラフも同様に考えることができます。

【アドバイス】

複雑な三角関数のグラフをかくときは，基本となるy＝sinθ，y=cosθ，y=tanθ のグラフをかき，それをどのように拡大，移動するかを考えるとよいです。そのときに，y＝asinb（θ-α）のグラフがy＝sinθのグラフをどのように拡大・縮小，平行移動したグラフであるかを，しっかり押さえておくことが大切です。
ただ，わからなくなってしまったときは，具体的に，例えばなどを代入して点をとり，基本となるグラフをどのように変形したかを考えてみてください。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。