【図形と方程式】等距離にあるx軸上の点の座標の求め方
等距離にあるx軸上の点の座標の求め方
2点A、Bから等距離なのでAP=BPということはわかるがAP^2=BP^2 にする意味がよくわからない。
√にしてといたらだめなの?
進研ゼミからの回答!
数学の勉強にがんばって取り組んでいますね。質問をいただいたのでお答えします。
【質問の確認】
【問題】
2点A(-2,1)、B(6,3)から等距離にあるx軸上の点Pの座標を求めよ。
について、
【解答解説】
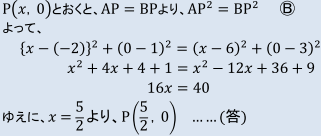
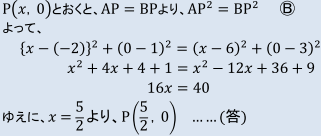
の1行目 ![]() のところについてですね。
のところについてですね。
【解説】
「AP2=BP2」 というように最初から2乗しておくのは、最初に 「 ![]() のつかない式」 にしておくと計算式が簡単になり、あとの計算が処理しやすいからです。
のつかない式」 にしておくと計算式が簡単になり、あとの計算が処理しやすいからです。
あなたが言うように、先に 「AP=BP」 を ![]() で表しておいてもOKですが、その式を簡単にするためには、結局 「両辺を2乗する」 という計算をしなくてはいけない
ということが予測できるので、それなら最初から2乗しておけばよいということでやっている計算なのです。
で表しておいてもOKですが、その式を簡単にするためには、結局 「両辺を2乗する」 という計算をしなくてはいけない
ということが予測できるので、それなら最初から2乗しておけばよいということでやっている計算なのです。
【アドバイス】
「2点間の距離」 というのは必ず 「 ![]() のついた式」 になるので、「2乗する」 という計算が必要になります。
のついた式」 になるので、「2乗する」 という計算が必要になります。
AP、BP は正の値をとるので、 「AP=BP」 ⇔ 「AP2=BP2」 となることをうまく利用していきましょう。
では、この調子でがんばってゼミの教材の問題に取り組み、実戦力を養っていってくださいね。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「図形と方程式」Q&A一覧
「図形と方程式」Q&A一覧
- 【図形と方程式】円の方程式の導き方
- 【図形と方程式】判別式の意味
- 【図形と方程式】接線の公式の使い方について
- 【図形と方程式】等距離にあるx軸上の点の座標の求め方
- 【図形と方程式】球の体積ってどうやって求めるの?公式の使い方と、なぜそうなるのかも知りたい












