ベネッセ
会員のかた

進研ゼミ 高校講座

【図形と方程式】接線の公式の使い方について

接線の公式の使い方について

円と直線の位置関係からでなく、接点の座標を設定して答えを求めるやりかたがわからない

進研ゼミからの回答！

こんにちは。
いただいた質問について、早速、回答します。

【質問の確認】

【問題】

点P(0，-1) を通り、円x2-6x+y2+4=0 に接する直線の方程式と、接点の座標を求めよ。

について、

【解答解説】

円と直線の位置関係からでなく、接点の座標を設定して答えを求める

解き方について、のご質問ですね。

【解説】

x2 -6x + y2 + 4 = 0
(x-3)2 + y2 = 5
なので中心(3，0)、半径 √5√5 の円です。

接線の公式を使うためには中心が原点でなければいけません。そこで円の中心が(0，0)になるように、平行移動した状態で接線を求め、それを逆に平行移動して元に戻すという手順で考えます。

x軸方向に‐3平行移動すると円はx2 + y2 = 5 になります。また問題では「(0，‐1)を通る」という条件でしたが、この(0，‐1)も同様にx軸方向に‐3平行移動すると、(‐3，‐1)になります。
そこで(‐3，‐1)を通り、x2 + y2 = 5 に接する接線を考えます。

【円の接線の方程式】

円x2 + y2 = r2上の点(x1，y1)における接線の方程式は
x1 x + y1 y = r2

接点の座標をP(x1，y1 ) とおくと、接線の方程式は

x1 x + y1 y = 5　･･･①

これが(‐3，‐1)を通るので

-3x1 - y1 = 5　･･･②

また点Pは円x2 + y2 = 5上の点なので

x12 + y12 = 5　･･･③

②よりy1 = -3x1 - 5　･･･④

④を③に代入すると

x12 + (-3x1 - 5)2 = 5

展開して整理すると

10x12 + 30x1 + 20 = 0

x12 + 3x1 + 2 = 0
(x1+2) (x1 + 1) = 0

よってx1 = -1，-2
x1 = -1のときy1 = -2
x1 = -2のときy1 = 1

これらを①に代入すると接線の方程式は

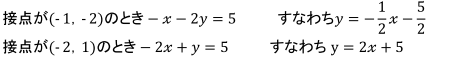
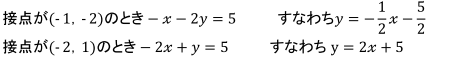
接点が(‐1，‐2)のとき-x-2y=5　すなわちy=-1/2 x-5/2　接点が(‐2，1)のとき-2x+y=5　すなわちy=2x+5 接点が(‐1，‐2)のとき-x-2y=5　すなわちy=-1/2 x-5/2　接点が(‐2，1)のとき-2x+y=5　すなわちy=2x+5

ただしこれは平行移動した後の接線なので、元に戻さなければいけません。
接点と接線をともにx軸方向に3平行移動します。

y=f(x)のグラフをx軸方向にpだけ平行移動したグラフを表す式はy=f(x-p)

なので接点が(‐1，‐2)のとき 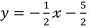y = -1/2 x - 5/2y = -1/2 x - 5/2 をx軸方向に3平行移動すると

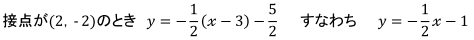
接点が(2，‐2)のとき　y=-1/2 (x-3)-5/2　すなわち　y=-1/2 x-1 接点が(2，‐2)のとき　y=-1/2 (x-3)-5/2　すなわち　y=-1/2 x-1

接点が(‐2，1)のとき y = 2x + 5 をx軸方向に3平行移動すると

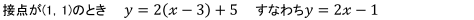
接点が(1，1)のとき　y=2(x-3)+5　すなわちy=2x-1 接点が(1，1)のとき　y=2(x-3)+5　すなわちy=2x-1

となります。

【アドバイス】

中心が原点ではない円で接点の座標を設定して求めるのは、添付の回答のように平行移
動が必要でかなり面倒になります。円と直線の位置関係を使う方が解きやすいと思います
ので、そちらの解き方を覚えておくとよいでしょう。

それではこれからも進研ゼミ　高校講座で実力アップを目指してくださいね。

2018年度入試 合格速報

進研ゼミで大学合格！
今年も喜びの声ぞくぞく！

読み込みに失敗しました。
進研ゼミ高校講座について詳しく見る

進研ゼミ『高校講座』関連商品・サービス

一番上に戻る

進研ゼミ 高校講座
会員向けページにようこそ

会員のかた
進研ゼミ 高校講座 ご受講のかた
保護者のかた
進研ゼミ 保護者通信

高校講座 オプションお申し込み(有料)

各種お手続き

受験プラン・コース変更、教科・科目の追加 登録内容(住所・電話番号・支払い方法など)の変更

受講に関するご質問ご相談など、お気軽にお問い合わせください。

受講に関するご質問ご相談など、お気軽にお問い合わせください。

※進研ゼミ『高校講座』について。矢野経済研究所「2014年版 教育産業白書」をもとに事業者を選定し、自社による第三者機関でのインターネット調査で高校生3,000人を対象に行った2015年4月時点で利用している学習法についての調査結果より。

学年をお選びください。

高校1年生 高校2年生 高校3年生
進研ゼミ ハイブリッドスタイル 利用環境条件

「進研ゼミ　ハイブリッドスタイル」はお手持ちのiPadでご利用いただけます。

対応機種
iPad（第4世代）、iPad Air、iPad Air 2、iPad mini 2、iPad mini 3、iPad mini 4
  • OS : iOS8.3以上。
  • 容量 : 8GB程度を想定。
  • 2016年2月時点。
  • 以下の端末ではお使いいただけません。
    パソコン、スマートフォン、iPad以外のタブレット、進研ゼミでお届けしている専用タブレット
    （チャレンジパッド、チャレンジタブレット、チャレンジタブレットネクスト）
通信環境

常時接続可能なブロードバンド（光ファイバなど）環境と、無線LAN（Wi-Fi）環境をご用意ください（10Mbps以上を推奨）。
  • 上記に合致しない環境では、サービスをご利用いただけない場合があります。
  • インターネットサービスプロバイダとの契約、無線LANルータが必要となります。接続料金等はお客さまのご負担となります。
  • セルラーモデルのiPadをご利用の方も、無線LAN(Wi-Fi)環境が必要です。ただし、テザリング機能での通信は推奨いたしません。
  • Apple、Apple ロゴ、iPadは米国および他の国々で登録された Apple Inc. の商標です。
  • iPadの機種、価格、内容等は変わることがあります。
  • ＜ハイブリッドスタイル＞で使用するiPadは、「進研ゼミ」以外のアプリにも接続できるタブレットです。インターネット接続・アプリ利用等の制限については、保護者の管理・判断のもとご利用ください。

あとから紹介制度のやり方

入会後に、ご紹介者の情報を登録することもできます。入会フォームの「入会後に、ご紹介者の情報を登録する」にチェックを入れてください。

Webでお申し込みをする場合

「入会申し込みページ」の「支払方法等の選択」内にある「ご紹介者」の欄で、 「入会後に、ご紹介者の情報を登録する」を選び、そのまま次の画面に進んでください。

  • Web画面のデザインはイメージです。変更する場合があります。

お申し込みの際にご登録いただいたメールアドレスに、手続き完了のメールをお送りしますので、プレゼント申し込み手続きを行う代表者を決め、お手続きをお願いします。

  • どちらかお一人がお手続きするだけでＯＫです。

電話でお申し込みをする場合

ご入会のお申し込みをいただく際、オペレーターが「ご紹介者はいらっしゃいますか」とおうかがいします。
⇒おそれいりますが「後から申し込みます」とお答えください。

入会完了

あなたと、あなたのお友だち・ごきょうだいに「教材」をお送りしますので、
プレゼント申し込み手続きを行う代表者を決め、0120-332211（9:00～21:00年末年始除く　通話料無料）までお電話ください。 ※一部のIP電話からは042-679-8567（ただし通話料がかかります）
その際、「お友だち・ごきょうだいの紹介であること」と「ご紹介者の会員番号」を忘れずにお伝えください。どちらかお一人がお手続きをすれば、お二人分のプレゼントをお届けします。

  • どちらかお一人がお手続きするだけでOKです。

「入会申し込みページ」の「支払い方法等の選択」内にある
「ご紹介者」の欄に、紹介してくれる方の情報をご入力ください。

紹介制度フォームサンプル

【お申し込み前に必ずお読みください】

●1月号（12/27まで）にご入会した方がキャンペーン対象です。
●受講費は1ヵ月分かかります。2月号以降を継続されない場合は、支払い期間にかかわらず「毎月払い」1ヵ月分の受講費のお支払いとなります。
●1ヵ月で退会する場合は1/10までに電話連絡が必要になります。ご連絡はお電話に限ります。
●退会連絡をいただかない場合、引き続き2月号以降をお届けします。

2019年12月17日に2021年度「大学入学共通テスト」にて予定されていた国語・数学の記述式問題の導入見送りの発表が文部科学省よりございました。現在「進研ゼミ高校講座」よりお届けしているご案内について、12月17日以前の入試情報でお届けしているものがございます。
今後お届けするご案内・教材については、最新の入試情報を踏まえてお届けできるように努めてまいりますので、ご理解のほど何卒よろしくお願い申し上げます。
なお、ベネッセコーポレーションでは、新大学入試の最新情報をわかりやすく解説する「教育セミナー」（参加費無料）を全国で開催しております。これから新入試に向けて頑張る高校生のみなさま・保護者の方に、ぜひ、ご活用いただけますと幸いです。
詳しくはこちらをご覧ください。