【図形と方程式】判別式の意味
判別式の意味
③の判別式をDとするとありますが、D≧0とは ③の式と円との共有点の個数をあらわしているのですか?
なぜここで判別式が出てくるのかわかりません・
進研ゼミからの回答!
こんにちは。
質問をいただきましたので、早速お答えしましょう。
【質問の確認】
【問題】
x2+y2≦4のとき、y-2xの最大値、最小値を求めよ。また、そのときのx、yの値を求めよ。
での判別式DやD≧0の意味について、ですね。
【解説】
円と直線の式を連立させて求めた方程式は、何を表すのでしょうか?
求めた方程式の実数解は、円と直線の共有点の座標を表します。
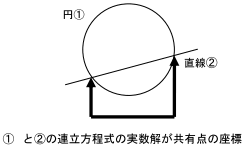

x2+y2≦4というのは円の周および内部(領域M)になります。
y-2x=k ・・・②とおいて、kの最大値と最小値を求めます。
円x2+y2=4 ・・・①として、この2つの方程式からyを消去すると、5x2+4kx+k2-4=0 ・・・③という方程式になります。
この実数解が共有点のx座標になりますが、判別式D≧0を考えることによって
直線②が円①に接するか異なる2点で交わるときを押さえているのです。この問題では「直線②が領域Mと共有点をもつ」という条件で考えるので、これを押さえる必要があるのですね。
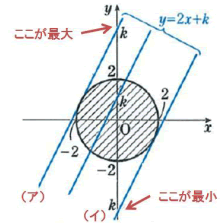

D≧0すなわち、![]() のとき 直線y-2x=kは上の(ア)から(イ)の範囲を動きます。求めるのはkの最大値と最小値なので、
のとき 直線y-2x=kは上の(ア)から(イ)の範囲を動きます。求めるのはkの最大値と最小値なので、![]() のとき最大値で、
のとき最大値で、![]() のとき最小値となるのです。
のとき最小値となるのです。
![]() のときは接するときで、直線②は(ア)であるときです。
のときは接するときで、直線②は(ア)であるときです。
![]() のときも接するときで、直線②は(イ)であるときになります。
のときも接するときで、直線②は(イ)であるときになります。
【アドバイス】
円と直線の方程式を連立させて求めた方程式の実数解は、何を表すのかをしっかり押さ
えておきましょう。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法












