【データの分析】修正したデータの値の求め方
修正したデータの値の求め方
修正によって,平均値が0.2大きくなるのでいずれか1つのデータが0.2×5=1だけ大きくなる,というところまでは,わかるのですが,そのあとが,よくわかりません。
進研ゼミからの回答!
がんばって教材に取り組んでいますね。 質問をいただいたのでお答えします。
【質問の確認】
次のデータは,ある高校の女子生徒5人の身長である。
160,162,156,165,161 (cm) ・・・・・・(∗)
(1) 中央値と平均値を求めよ。
(2) 上のデータのうち,1つの数値が測定ミスで間違っていることがわかった。修正した正しい数値で計算し直すと,中央値は162cm,平均値は161cmとなった。間違っていた数値とその正しい数値を求めよ。
の(2)について,
(2) 修正によって,平均値が,
161−160.8=0.2(cm)
大きくなっているので,(∗)のデータのいずれか1つが,
0.2×5=1(cm)
だけ大きくならなければならない。 ・・・・・・(★)
また,修正後のデータの中央値が162cmとなることにより,
156,160,161
のいずれか1つが1cmだけ大きくなればよい。
ここで,
156,160
の2つの数値は,いずれも1cm大きくなっても,中央値は161cmのままなので,条件に合わない。
よって,161cmが1cm大きくなって162cmになると,データは,
156,160,162,162,165
となり,条件を満たす。
ゆえに,
間違っていた数値は161(cm),正しい数値は162(cm) ・・・・・・(答)
解答の修正によって,平均値が0.2大きくなるのでいずれか1つのデータが0.2×5=1だけ大きくなる, というところまで(解答の(★)部分まで)は,わかるのですが,そのあとが,よくわかりません。
というご質問ですね。
【解説】
≪解答の方針を考える≫
(1)で,間違っている数値での平均値:160.8(cm),中央値:161(cm)とわかりました。
そこで,解答の(★)より,
「平均値が 161cm を満たすには,どれか1つのデータが 1 cm 大きくなればよい」
と言えます。ここまでは大丈夫でしょうか? これより,次は,
5つのうち,どのデータを 1 cm 大きくすれば,「中央値が 162cm」 を満たすのか ・・・★
を考えます。
中央値というのは,
「データを値の小さい順に並べたとき,中央の位置にくる値」
のことなので,ここでは,
5つのデータの中央の位置にあたる,3番目のデータの値が中央値
になります。
与えられたデータを小さい順に並べると,
「156,160,161,162,165」
となるので,中央値は 「161cm」となっています。 そこで,上記★の
5つのうち,どのデータを1cm大きくすれば,「中央値が 162cm」 を満たすのか
を考えていきましょう。 ここでは,
「中央値である161cmより大きい162や165を1cm大きくしても,中央値は161cmのままで変わらない」
ということがわかります。ですから,解答のように,
「156,160,161」のいずれか1つが1cm大きくなればよい
と言えるのです。
≪条件を満たす場合を具体的に考える≫
そこで,順番に1cm大きくして,条件を満たすかどうかを考察してみましょう。


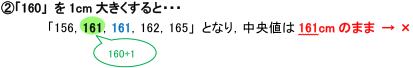
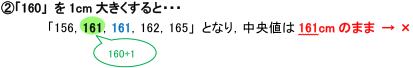


よって,「161を1cm大きくすればよい」 ということがわかるのです。
【アドバイス】
「中央値」 というのは,「データを値の小さい順に並べたとき,中央の位置にくる値」であることをここでしっかり頭に入れておきましょう。
では,この調子でがんばって『進研ゼミ高校講座』の問題に取り組み,実戦力を養っていってくださいね。
応援しています!
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
 「データの分析」Q&A一覧
「データの分析」Q&A一覧
- 【データの分析】ヒストグラムが与えられたデータから,中央値を求める方法
- 【データの分析】修正したデータの値の求め方
- 【データの分析】四分位数の求め方
- 【データの分析】無理数の近似値の求め方
- 【データの分析】相関係数の求め方
- 【データの分析】箱ひげ図のかき方












