【波の性質】y-xグラフとy-tグラフが描けないです！

【質問の確認】

≪y−xグラフとy−tグラフが描けないです！≫
y−xグラフとy−tグラフがどっちがどっちだかイメージできません。
解説を見ても，y方向正の向きに変位するとか，負の向きに変位するとかが，よくわかっておりません。

【解説】

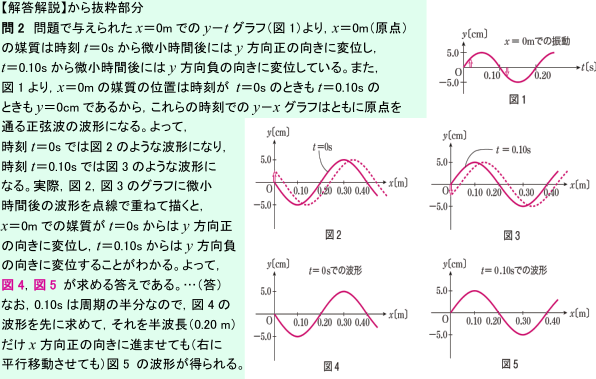
波とは，媒質の振動が次々に伝わっていく現象です。波には「ある位置（例えば原点）での媒質に注目し，その媒質の振動をグラフにしたものがy−tグラフ」（図1）と，「ある時間での媒質の変位を写真のように写したものが，波の形（波形）を表すy−xグラフ」(図2)があります。

サッカーの観客席で起きるウェーブを想像してみてください。ある瞬間に観客席にできた波を写真に撮ったものがy−xグラフ，１人の観客が立ったり座ったりするのをビデオで撮ったものが，y−t グラフです。

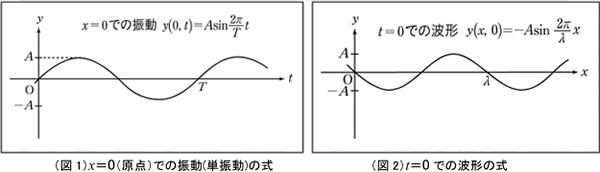
(図1)はx＝0の位置にある媒質の，時刻tにおける変位（高さ）の変化を表しています。そして，（図2）はt＝0で見える波の形，つまり『波形』を表しています。しかし，波は動くものなので，(図2)の波形は一瞬で，すぐに変化していきます。よって，あらゆる場所における，あらゆる時間の波の高さがわかるような式を「波の式」といい，

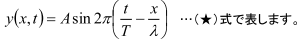
ここで重要なのは，波の式（★）において，変数はx (位置)，t（時間）の2つで，それ以外（A，λ，t)は定数だから，xとtを代入すれば，変位yが求まるということです。このように，波は変数が2つある『2変数関数』なので，xを固定した（例えばx＝0）y−tグラフと，tを固定した（例えばt＝0）y−xグラフに分けて描くのです。
次に，「波がy方向の正の向きに変位するのか，負の向きに変位するのか」について考えていきます。

(ⅰ) y−tグラフの場合
先ほど記述したように，y−tグラフは，ある位置（例えば原点）での媒質の振動を表しているので，時間軸に沿って，つまりt 軸に沿って，微小時間経過したとき，yが正・負どちらに変位したかを見極めればわかります。

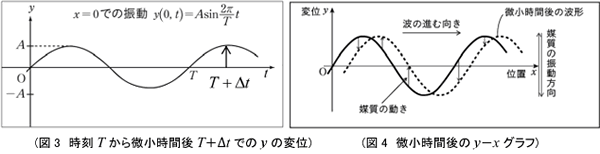
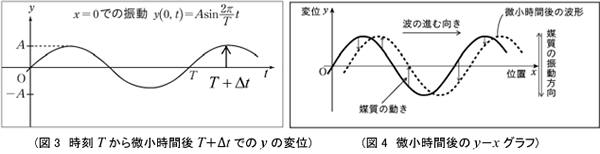
図3の場合，t＝T で y＝0であったのものが，t＝T＋Δtでy＞0となったので，yは正の向きに変位したことになります。

(ⅱ) y−xグラフの場合
y−xグラフは，ある時間での波の形（波形）を表しているので，「微小時間後の波形のグラフを描いて考える」ことがポイントとなります。(図4)のように，ある位置xでの，微小時間後の波形が変位 y（点線の波形）として表されるので，媒質が上向きに動いていれば，正の向きに変位，下向きに動いていれば負の向きに変位したとわかります。

【アドバイス】

波のグラフを考える場合は，
・「ある位置（例えば原点）での媒質の振動のy−tグラフ」なのか，
・「ある時間での波の形（波形）のy−xグラフ」なのか，しっかりと確認をしましょう。
この回答を参考にこの問題にもう一度挑戦しておくとよいと思います。
これからも進研ゼミ高校講座にしっかりと取り組んでいってくださいね。