【複素数と方程式】虚数「i 」

【質問の確認】

虚数「i」が具体的にイメージできず，よくわかりません。そもそも，なんで虚数なんて数が出てくるのでしょうか。
というご質問ですね。

【解説】

虚数は，想像上の数。つまり，実数のように，実際には大きさなどが見えない数です。初めてこのような概念に触れるみなさんにとってわかりにくくて当然です。
そこで，ここでは，
１．虚数とは
２．なぜ虚数を使うのか
３．虚数を含む計算をするときのポイント
を説明しますので，じっくり読んでください。

≪１．虚数とは≫
虚数は「Imaginary number」といい，文字通り，想像上の数です。実数は，数直線上に表せるなど，実際に目に見えるからわかりやすいですが，虚数は大小関係がないので，普通の数直線上には表せないのです。

≪２．なぜ虚数を使うのか≫
では，このようにイメージしにくい虚数をなぜ考えるのでしょうか？
例えば，２次方程式x²-3x+4=0を解くとき，解の公式を使うと，

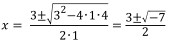
このように， の中が負の数になるので，実数の範囲で考えると「解なし」となります。
そこで，２乗すると−１になるiという数（虚数単位という）を考え出して，a，biを実数として，a+biという形で表せる虚数を形式的に導入しました。これによって，２次方程式は虚数解も含めて必ず解をもつといえるようになりました。つまり，

そこで，上の方程式は，「という解をもつ」のです。（これを複素数といいます。）

≪３．虚数を含む計算をするときのポイント≫
最後に虚数の計算方法についてです。ポイントは３つです。

★ポイント1★　「i がない部分（実部）」と「i がある部分（虚部）」に分けて計算する！

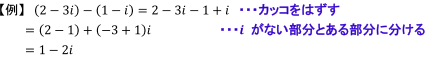
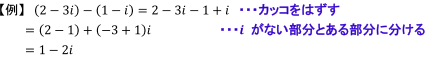
★ポイント２★　i² が出てきたらi² =-1という定義より，i² を−1に置き換える！
★ポイント３★　i が出てきたら，文字と同じように扱って計算する！
普通の a や x などの文字と同じように扱います。

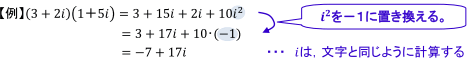
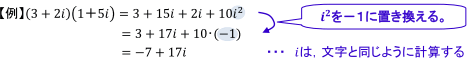
この３つの計算方法のポイントは使えるようになっておきましょう。

【アドバイス】

虚数は，新たな数の概念なので難しいかもしれませんが，定義と計算のポイントをしっかりと押さえて，今後使えるようになってくださいね。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。