【数列】等比数列の和について
等比数列の和について
例題の解答で、
1･1 + 1･3 + 1･3＾2 + 1･3＾3 + .... + 1･3＾n−1
は、初項 1、公比 3、項数nの等比数列の和と書いてあるのですが、なぜ項数はn−1 ではなくnになるんですか。
進研ゼミからの回答！
こんにちは。
質問をいただいていましたのでお答えします。
【質問の確認】
【問題】
次の和Sを求めよ。
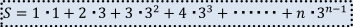
という問題の
において、
のところで、なぜ項数は、n-1ではなくnか、ということですね。
【解説】
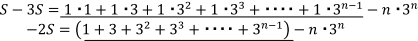
はいいですね。
1･1 + 1･3 + 1･32 + 1･33 + ・・・・ + 1･3n-1
＝1 + 3 + 32 + 33 + ・・・・ + 3n-1
ですから、1 + 3 + 32 + 33 + ・・・・ + 3n-1 の項数を考えます。
1 + 3 + 32 + 33 + ・・・・ + 3n-1
＝30 + 31 + 32 + 33 + ・・・・ + 3n-1
と表して、３の指数に注目します。
すると、
0、1、2、3、・・・・・・・・、n-1
で、0 から n-1 まで「n個」ですから、項数はnとわかります。
したがって、1 + 3 + 32 + 33 + ・・・・+ 3n-1 は
初項１、公比３の等比数列の初項から、第n項までの和となります。
【アドバイス】
項数については、一目では求められない場合がありますが、このように、指数を書き直してみたり、あらためて書き並べて見やすくすることによってわかりやすくなる場合がありますので、参考にしてください。
これからも「進研ゼミ 高校講座」でがんばりましょう。
数学のQ&Aランキング
全体のQ&Aランキング
「数列」Q&A一覧
他の教科のQ&Aを見る【その他にも苦手なところはありませんか？】
わからないところをウヤムヤにせず、その場で徹底的につぶすことが苦手を作らないコツ。
「進研ゼミ」には、苦手をつくらない工夫があります。
＜進研ゼミでできること＞授業やテスト前の「わからない」を解消・苦手をつくらない
教科書別に要点をおさえて
予習復習も効率的に！
個人のニガテをAIが分析。
力が伸びる問題を自動出題。
