【微分法(III)】置き換えによる微分

【質問の確認】

上の問題の解答を見ると，u=2x+1とおいているのですが，どうしてこのような解き方をするのですか？
というご質問ですね。

【解説】

この問題では，y=(2x + 1)³+(2x+1) の右辺を展開してから微分する，という解き方もできます。
ところが，例えば，(2x ＋ 1)⁵のように次数が高い式になると，展開が煩雑になり，ミスの原因にもなりかねません。そこで，より効率よく計算ができるように工夫しているのです。では，その解き方について解説していきましょう。

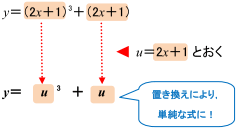
与えられた関数をよく見ると．「2x＋1」という共通なカタマリが見えますね。
そこで，これをuとおくと，この関数は，y = u³ + u という u の３次関数と見ることができます。
このように，より単純な式にしてから微分する方が計算しやすいですね。

さて，ここで，u ＝ g(x) ＝ 2x ＋ 1，f(u) ＝ u³ ＋ u とおくと，与えられた関数y = (2x + 1)³ + (2x+1) は，y＝f(g(x)) となり，y ＝ f(u) と u ＝ g(x) の合成関数と見ることができます。そして，合成関数の導関数には，次の公式が成り立ちます。

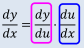
これを利用して解くと，次のようになります。
まず，

では，微分の仕方をまとめておきましょう。

---

≪合成関数の導関数の公式≫
合成関数は，(外側の関数を微分)×(中の小さい関数を微分)×(さらにその中の関数を微分)×……というように，外から内へドンドン微分して掛ける，と考えます。
①を例にとってみると，次のようなイメージです。

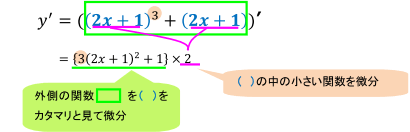
このように考えると，2x＋1をu とおいてステップを３回踏まなくても，一気に微分できてしまいます。
ポイントは，

・カタマリをつくり，外側の関数と中の小さな関数をとらえる

・外側から微分する

です。

【アドバイス】

次数が高い式など，y ＝ f(g(x)) の形をしているときは，「合成関数の導関数」の公式を確実に利用できるようにしておきましょう。まずは，u ＝ g(x) とおいて，3ステップで確実に解けるように練習しておきましょう。
慣れてくれば，

・カタマリをつくり，外側の関数と中の小さな関数をとらえる

・外側から微分する

というポイントを押さえ一気に微分してもよいでしょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。