【関数と極限】数列の極限について

【質問の確認】

数列の極限を求める問題で，値を代入してやとなったから1，∞−∞となったから0としたら答えが違ってしまうのはどうしてですか。

というご質問ですね。

【解説】

極限を求める式は，例えば，

と書きますが，xは1という値そのものになるのではなく，あくまでも，xを1に限りなく近づけたら，x＋3は4に限りなく近づく，つまり，
x →1のとき，x＋3 →4
という状況を考えています。
また，∞は，限りなく大きいことを表す記号であって，限りなく大きな数値ではありません。x →∞は，変数xが限りなく大きくなる状況を表しているのです。

つまり，極限を求めるときは状況を考えてみるとよいということです。これを踏まえて，次のようなステップで極限を求めてみましょう。

 

≪Step 1　変数が限りなく大きくなると，どんな状況になるかを確認する≫

 

≪Step 2　変数が限りなく大きくなると となる場合は，工夫して式変形をする≫

 

≪Step 2′　 となる場合に直感的に極限を予想する≫

発散するスピードに着目し，直感的に極限を予想することも大切です。
例えば，， と，どちらも（正の）無限大に発散しますが，そのスピードを考えると，n²の方が速いというのは直感的に明らかですね。ここに着目すると，となることが予想できます。
また，なら，分母と分子の（正の）無限大に発散するスピードを考えると，分子の２次の項の係数が，分母の ２次の項の係数の２倍になっているので，分子が分母のほぼ２倍であることが想像できます。よって，極限が２になると予想できます。

 

≪Step 3　直接極限がわかる形に式変形できないときは，はさみうちの原理を利用する≫

まず，はさみうちの原理を確認しておきましょう。

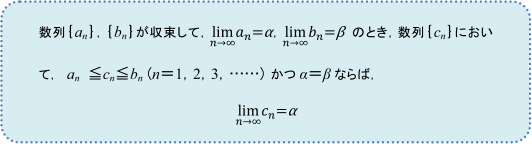
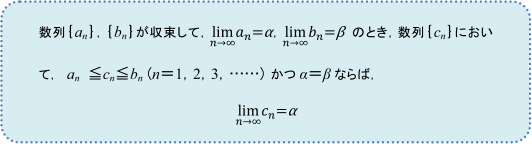
【例３】 のように，直接極限がわかる形に式変形できないときは，極限値のわかる数列，を利用して，an ≦cn≦bn という不等式をつくり，「はさみうちの原理」を利用します。具体的に考えてみましょう。

---

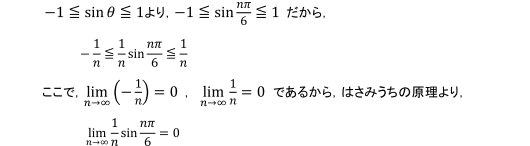
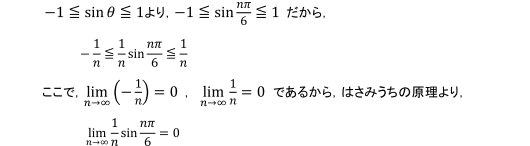
◎まとめ
極限を求めるときは，上の３つのStepを考えましょう。
やとなったから1，∞−∞ となったから0とは限らないので，やや∞−∞になる場合は注意する必要があります。

【アドバイス】

変数が限りなく大きくなるとやや∞−∞の形になる場合の極限は，工夫して式変形したり，「はさみうちの原理」を使ったりする必要がありますね。多くの問題を解いて，どのような場合にどのような工夫が必要なのかを身につけてください。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。