【平面ベクトル】内積の求め方
内積の求め方
「直角三角形において,内積AB→・BC→ を求めよ。」という問題で,
定義にあてはめて,AB→・BC→=|AB→||BC→|cosB=2・√3cos30°=3 としたのに,正しい答えが出ません。 どこが間違っていますか?
進研ゼミからの回答!
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
【問題】


上の問題で,定義にあてはめて,![]() としたのに,正解は,−3でした。どこが間違っていますか?
としたのに,正解は,−3でした。どこが間違っていますか?
というご質問ですね。
【解説】
まずは,定義を振り返っておきましょう。
【内積の定義】
![]() でない2つのベクトル
でない2つのベクトル![]() ,
,![]() のなす角がθのとき,
のなす角がθのとき,
![]()
上の解答では,確かに,辺の長さをあてはめていますが,残念ながら,内積の定義を使うときの重要なルールに従っていません。
2つのベクトルのなす角を求めるときに重要なことは,「ベクトルの始点を合わせる」ということです。
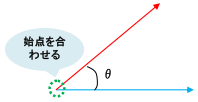

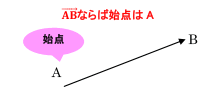
ベクトルの始点とは,![]() ならば点A,
ならば点A,![]() ならば点Bのことです。
ならば点Bのことです。
つまり,ベクトルの始まりにある(左側にある)文字で表される点のことです。

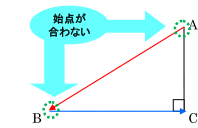
上の解答では,![]() と
と ![]() の大きさとなす角を30°として計算していましたが,
の大きさとなす角を30°として計算していましたが,![]() と
と ![]() のなす角は30°ですが,
のなす角は30°ですが,![]() と
と ![]() のなす角は30°ではないのです。
のなす角は30°ではないのです。

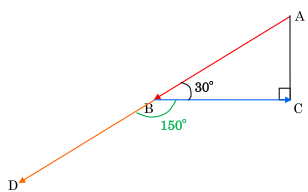
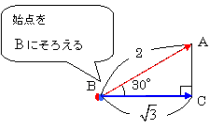
そこで,![]() を平行移動して,
を平行移動して,![]() の始点を
の始点を ![]() の始点のBにそろえます。
の始点のBにそろえます。
すると,![]() と
と ![]() のなす角は,下の図で
のなす角は,下の図で![]() =
= ![]() ですから,
ですから,![]() と
と ![]() のなす角となり,180°−30°=150°とわかります。
のなす角となり,180°−30°=150°とわかります。

よって,
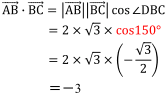
また,始点の合わせ方により,次のような別解も考えられます。
【別解1】![]() を平行移動して,始点をAにそろえる方法
を平行移動して,始点をAにそろえる方法
![]() を平行移動して,図のように,始点をAにそろえると,
を平行移動して,図のように,始点をAにそろえると,
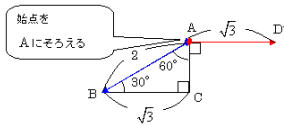

![]()
【別解2】 ![]() =
= ![]() と書きかえる方法
と書きかえる方法
![]() の向きを逆にして,
の向きを逆にして,![]() =-
=-![]() を利用すると,
を利用すると,
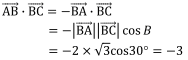
となります。
内積の定義を使うときは,「始点を合わせる」ということに注意しましょう。

【アドバイス】
定義や定理は正しく理解し,正しく使うことが大切です。今後もいろいろな定義や定理を学習すると思うので,その定義や定理を利用する問題を解きながら,正しく理解するように心がけましょう。
また,今回のようにどこで間違えているかわからないときは,それをそのままにせず,どこが違うのかを必ず明らかにすることが大切ですね。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
 数学のQ&Aランキング
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法
- 【図形と計量】180°-θの三角比
 全体のQ&Aランキング
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞+∞=∞とは
- 【三角関数】0<θ<π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを(1/a)^r の形になおす方法












