【平面ベクトル】ベクトルの表し方
ベクトルの表し方
Ｄの解説には
「ベクトルＯＡ、ベクトルＯＢはともに０ベクトルでなく平行でないので、ベクトルＯＰをこのようにおくことができる」
と書いてあるのですが、なぜそうおけるのか、わかりません。
どういったときに、ベクトルＯＰ＝sベクトルＯＡ＋tベクトルＯＢのように表せるのか、詳しく教えてください。
進研ゼミからの回答！
こんにちは。チャレンジ数学を利用して授業対策に励んでいますね。しっかり理解していきましょうね。
では、いただいたご質問にお答えいたしましょう。
【質問の確認】
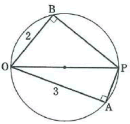【問題】
直径OPの円に四角形ＯＡＰＢが内接していて、OA=3、OB=2であり、
= 2 である。このとき、
を用いて表せ。
という問題の解答の最初の立式と解説
【解答解説】
(s、tは実数) ･･････①とおける。
はともに 
でなく平行でないので、
をこのようにおくことができる。
についての質問ですね。
【解説】
２つのベクトル 
、
において、 ≠ 
、 ≠ 、 ≠ のとき ･･････（＊）
平面上の任意のベクトル 
は、 = s + t （s、tは実数）の形にただ１通りに表される。
つまり、
、
が（＊）の条件を満たしていれば、常に
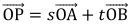
と表せるのです。
これは、
を対角線とする平行四辺形を作ってみるとわかりやすいですよ。
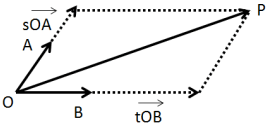
（＊）を満たしていればこのように必ず平面上の任意のベクトルは
とを使って表すことができますね。
【アドバイス】
今回のベクトルの表し方については、
平行四辺形をイメージして図形的に捉えていくといいですよ。
そして、ご質問の問題についてもう一度考えておきましょうね。
また、様々な問題に取り組んで慣れていくといいでしょう。
「進研ゼミ高校講座」の教材を利用して練習していきましょうね。
そして、また何か疑問に思うことが出てきましたら、質問してくださいね。
数学のQ&Aランキング
- 【数列】Σの和の求め方
- 【関数と極限】∞＋∞＝∞とは
- 【三角関数】0<θ＜π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを（1/a）＾r の形になおす方法
- 【図形と計量】180°-θの三角比
全体のQ&Aランキング
- 【動名詞】①<make + O + C >構文の訳し方②間接疑問文における疑問詞の訳し方
- 【数列】Σの和の求め方
- 【関数と極限】∞＋∞＝∞とは
- 【三角関数】0<θ＜π/4 の角に対する三角関数での表し方
- 【指数・対数関数】1/√aを（1/a）＾r の形になおす方法
「平面ベクトル」Q&A一覧
他の教科のQ&Aを見る
【その他にも苦手なところはありませんか？】
わからないところをウヤムヤにせず、その場で徹底的につぶすことが苦手を作らないコツ。
「進研ゼミ」には、苦手をつくらない工夫があります。
＜進研ゼミでできること＞授業やテスト前の「わからない」を解消・苦手をつくらない
教科書別に要点をおさえて
予習復習も効率的に！
個人のニガテをAIが分析。
力が伸びる問題を自動出題。
