【数と式】必要条件・十分条件

【質問の確認】

必要条件・十分条件がわかりません。
というご質問ですね。

【解説】

まず，必要条件・十分条件の定義を確認しましょう。

これは基本になるのでしっかり覚えてください。また，次のように図式的に書いて，矢印の先は必要と覚えてもよいです。

ここで，重要になるのが，p ⇒ q，q ⇒ pが真であるか偽であるかということです。そこで，p ⇒ qの真偽の調べ方を確認しましょう。

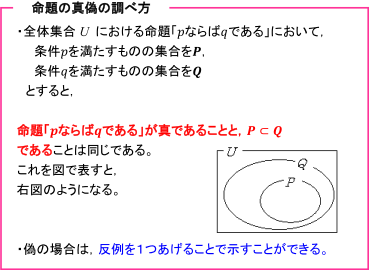
では，具体的な例で考えていきましょう。

【例１】
ぶどうと果物の関係を考えてみましょう。

Step１ぶどう ⇒ 果物を考える
ぶどうは果物です。
ぶどうは果物だし，「植物」だし，……と，いろいろと言うことはできますが，そのうちの１つとしてぶどうならば果物ということは確実に言えます。つまり， ぶどうであることは果物であることを保障する十分な条件と言えますね。

Step２果物 ⇒ ぶどうを考える
逆に，果物ならばぶどうとは言えません。例えば，果物には「りんご」，「いちご」，……と，ほかにもいろいろあるためです。

Step３　Step１，２より，必要条件・十分条件・必要十分条件を考える
ここで，図をかいて考えてみると，下のようになるので，

このことからも
ぶどう ⇒ 果物が真
果物 ⇒ ぶどうが偽
であることがわかります。

よって，Step１，Step２より，
ぶどうは，果物であるための十分条件
果物は，ぶどうであるための必要条件
となります。

【例２】次に，x²＝1とx＝1を考えてみましょう。
Step１  x²＝1 ⇒ x＝1の真偽を調べます。
x²＝1を解くと，x＝±1です。
よって，x＝-1が反例になるので，
x²＝1 ⇒ x＝1は偽です。

Step２  x＝1 ⇒ x²＝1の真偽を調べます。
x＝1のとき，x²＝1²＝1だから，
x＝1⇒ x²＝1は真です。

Step３ Step１，２より，必要条件・十分条件・必要十分条件を考えます。
真である命題は「x＝1⇒ x²＝1」だから，
x²＝1は，x＝1であるための必要条件
x＝1は，x²＝1であるための十分条件

となります。

【アドバイス】

必要条件・十分条件を判断するには，まず，p ⇒ q，q ⇒ pの真偽を考えなければならないので，命題の真偽の判断をしっかりできるようにしてください。

そして，真である命題に着目して，必要条件・十分条件を判断しましょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。