【数と式】逆・裏・対偶の関係

【質問の確認】

逆・裏・対偶の関係がわかりません。というご質問ですね。

【解説】

逆・裏・対偶を書くには，単純に，入れ替えたり，￣をつければ(条件の否定をつくれば)いいだけです。
まず，逆・裏・対偶の定義を確認しましょう。

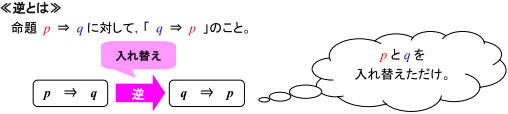
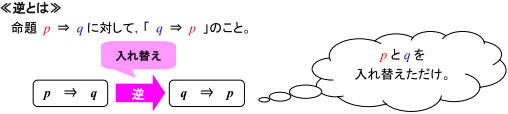
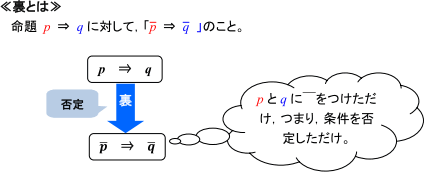
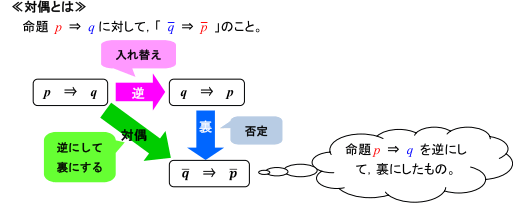
そして，これらの関係図を示すと下の図のようになります。
両方向の矢印になっているのは，その逆の方向も成り立つことを示します。

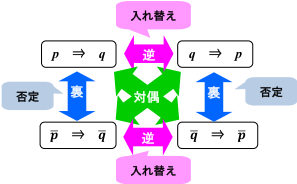
これらは基本となるのでしっかり覚えてください。

---

【つまずきやすいポイント】
次に，つまずきがちなポイントについて説明しましょう。
よくつまずいてしまうポイントは，逆・裏・対偶にしたときの「真偽」を気にしてしまい，逆・裏・対偶自体がわからなくなることです。
逆，裏，対偶となる命題を述べることと，その命題の「真偽」を考えることは，全く別の話です。
「命題 x＝1 ⇒ x²＝1の逆を言え。」という問題ならば，「 x²＝1 ⇒ x＝1 」とすればよいのです。
「次の命題の逆・裏・対偶をつくり，その真偽を言え。」などという問題では，

１．まず，逆・裏・対偶を書く。

２．それから，それぞれの命題について，真偽を考える。

というように，分けて考えましょう。

例えば，「命題 x＝1 ⇒ x²＝1の逆をつくり，その真偽を言え」という問題では，

１．逆を書く。・・・ x²＝1 ⇒ x＝1（条件を入れ替える。）

２．1の命題の真偽を考える。・・・x²＝1を解くと，x＝±1　よって，x＝-1が反例となるので真ではない，つまり偽。

◎オマケ◎

命題「 」とその対偶「 ) 」は，「真偽」が常に一致します。
だから，「命題『 』が真である」ことを証明するために，その対偶「 」が真であることを示せばOKです。
命題を直接証明しにくいとき，その命題の対偶を証明するという手法は，よく使われます。
（このような証明方法を間接証明法といい，背理法による証明もその１つです。）

【アドバイス】

逆・裏・対偶の定義をしっかり理解しておきましょう。
また，裏と対偶では，条件の否定を使うので，否定のつくり方も復習しておくとよいでしょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。