【図形と計量】sin，cos，tanの値の覚え方

【質問の確認】

sinθ，cosθ，tanθの値を導こうとすると，間違えてしまいます。この値を覚える方法はありませんか？
というご質問ですね。

【解説】

≪三角比の値の求め方≫
sinθ，cosθ，tanθの値は，次の「よく出る２つの三角形」と「sinθ，cosθ，tanθの定義」を覚えていれば導けます。

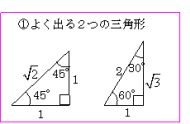
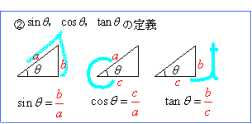
【これらを使った求め方】

①θの値（角度）を見て，「よく出る２つの三角形」のうち，当てはまる三角形をかき出す。

②「sinθ，cosθ，tanθの定義」を三角形に当てはめて，辺の比を導く。

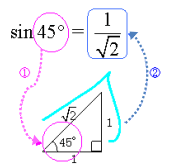
ただし，このように導くことがニガテな人は，次のように覚えてしまってもよいでしょう。

≪三角比の値の覚え方≫
まずは，0°から90°までの角の三角比の値について覚えましょう。
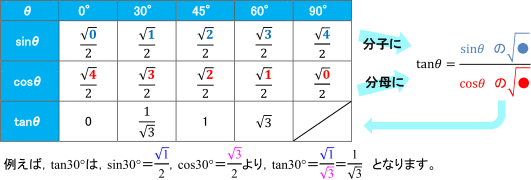
覚えておくべきθの値は，0°，30°，45°，60°，90°です。 sinθ，cosθの値をすべての形で書くことにすると，次のようになります。

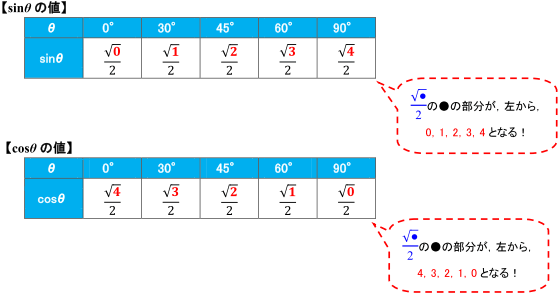
【tanθの値】
tanθについては，sinθ，cosθほど簡単な覚え方はありませんが，次の２つの方法のうち，どちらか好きな方で覚えるとよいでしょう。
＜その1＞tanθの値を暗記する
　次の値を暗記しておく方法です。よく見ると，それほど複雑な値ではありませんね。

＜その2＞tanθの値の導き方で覚える（sinθ，cosθの表を使う）
sinθ，cosθの表をかき出した後，として，値を計算します。表の上の段（sinθの段）が分子，下の段（cosθの段）が分母なので，覚えやすいですね。

≪180°までの三角比の値の覚え方≫
さて，ここまでは90°以下の角について見てきました。ここからは，90°から180°までの三角比の値について見ていきましょう。これも規則を覚えると簡単です。90°を境に，次のような規則になります。

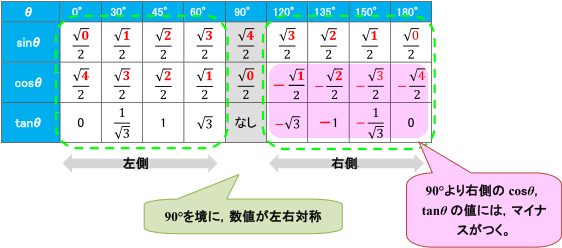
テストが始まったら，この表を問題用紙の端にかき出しておくとよいでしょう。

【アドバイス】

今後，0°，30°，45°，60°，90°，120°，135°，150°，180°の三角比の値は，よく利用します。今のうちに正しい値を求められるようにしておくか，きちんと覚えておくようにしましょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。